The Lean Theorem Prover

Leonardo de Moura (Microsoft Research),
Soonho Kong (CMU), Jeremy Avigad (CMU),
Floris van Doorn (CMU), Jakob von Raumer (KIT),
Rob Lewis (CMU), Haitao Zhang,
Daniel Selsam (Stanford)

CADE, 2015/08/07
http://leanprover.github.io

Many thanks to

  • Cody Roux
  • Georges Gonthier
  • Grant Passmore
  • Nikhil Swamy
  • Assia Mahboubi
  • Bas Spitters
  • Steve Awodey
  • Ulrik Buchholtz
  • Tom Ball
  • Parikshit Khanna

Introduction: Lean

  • New open source theorem prover
  • Platform for
    • Software verification & development
    • Formalized mathematics
    • Education (mathematics, logic, computer science)
    • Synthesis (proofs & programs)
  • de Bruijn's Principle: small trusted kernel
  • Expressive logic based on dependent type theory
  • Partial constructions: automation fills the "holes"

Introduction: Lean

Main Goal

Lean aims to bring two worlds together

  • An interactive theorem prover with powerful automation
  • An automated reasoning tool that
    • produces (detailed) proofs,
    • has a rich language,
    • can be used interactively, and
    • is built on a verified mathematical library

Secondary Goals

  • Minimalist and high-performace kernel
  • Experiment with different flavors of type theory
    • Proof irrelevant vs Proof relevant
    • Impredicative vs Predicative
    • Higher Inductive Types
    • Quotient Types
    • Observational Type Theory
  • Have Fun

What is new?

  • Poweful elaboration engine that can handle
    • Higher-order unification
    • Definitional reductions
    • Coercions
    • Ad-hoc polymorphism (aka overloading)
    • Type classes
    • Tactics

"By relieving the brain of all unnecessary work, a good notation sets it free to concentrate on more advanced problems, and in effect increases the mental power of the race." – A. N. Whitehead

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
    • It does not contain
      • Termination checker
      • Fixpoint operators
      • Pattern matching
      • Module management
    • Reference type checker
      • Implemented by Daniel Selsam
      • < 2000 lines of Haskell code
      • Code is easy to read and understand
      • Type check the whole standard library (35K lines) under 2 mins
    • All Lean files can be exported in a very simple format

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
  • Multi-core support
    • Process theorems in parallel
    • Execute/try tactics (automation) in parallel

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
  • Multi-core support
  • Fast incremental compilation

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
  • Multi-core support
  • Fast incremental compilation
  • Support for mixed declarative and tactic proof style

What is new?

  • Poweful elaboration engine that can handle
  • Small trusted kernel
  • Multi-core support
  • Fast incremental compilation
  • Support for mixed declarative and tactic proof style
  • Quotient types

Architecture

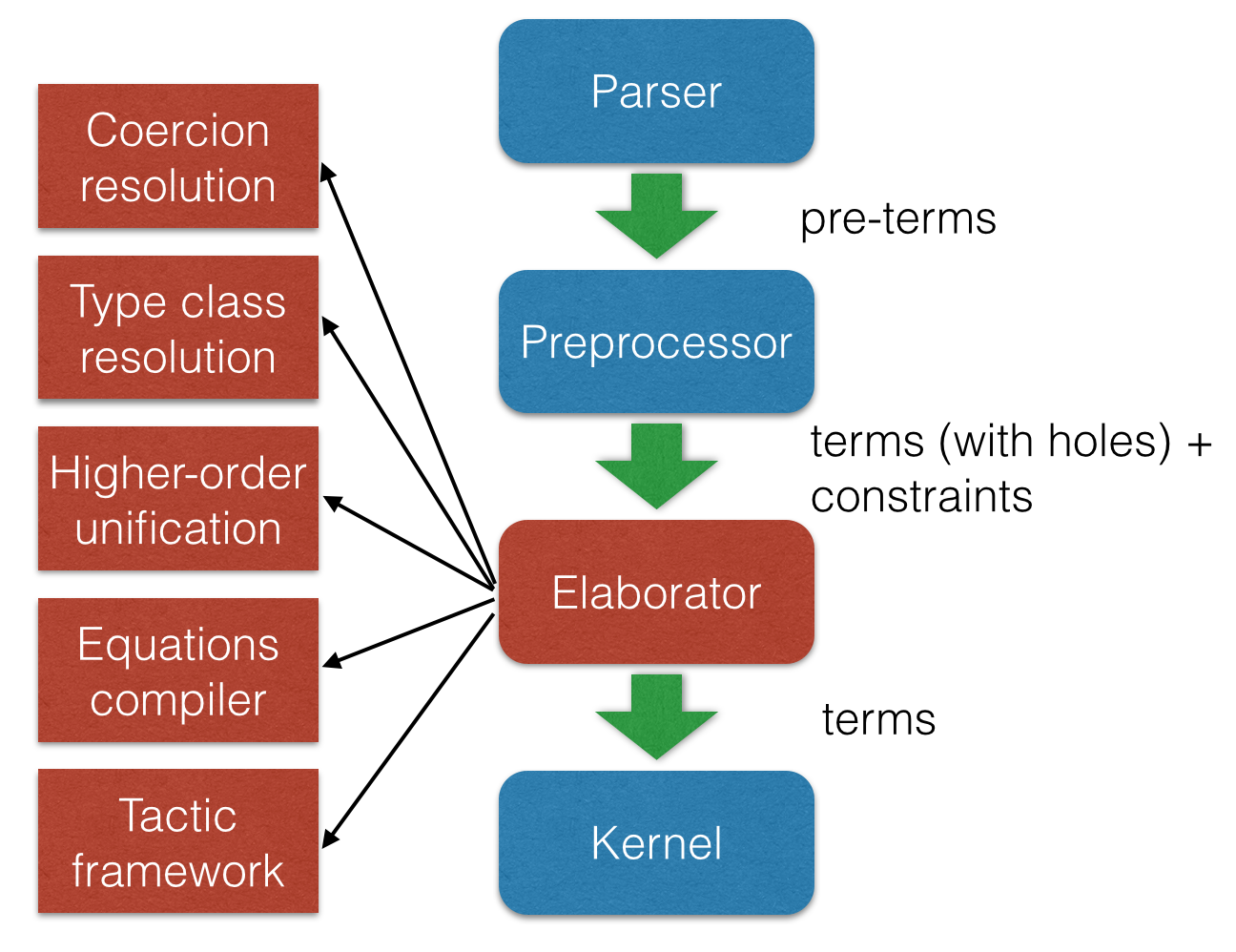
framework2.png

Two official libraries

  • Standard
    • Proof irrelevant and impredicative Prop
    • Smooth transition to classical logic
    • Inductive Families
    • Quotient Types
  • HoTT
    • Proof relevant and no impredicative Prop
    • Univalence axiom
    • Inductive Families
    • HIT
  • Easy to implement experimental versions, Example: Steve Awodey asked for proof relevant and impredicative universe

Recursive equations

  • Recursors are inconvenient to use.
  • Compiler from recursive equations into recursors.
  • Two compilation strategies: structural and well-founded recursion
definition fib : nat → nat | fib 0 := 1 | fib 1 := 1 | fib (a+2) := fib (a+1) + fib a example (a : nat) : fib (a+2) = fib (a+1) + fib a := rfl

Recursive equations

  • Dependent pattern matching
definition map {A B C : Type} (f : A → B → C) : Π {n : nat}, vector A n → vector B n → vector C n | map nil nil := nil | map (a::va) (b::vb) := f a b :: map va vb definition zip {A B : Type} : Π {n}, vector A n → vector B n → vector (A × B) n | zip nil nil := nil | zip (a::va) (b::vb) := (a, b) :: zip va vb

Human-readable proofs

import algebra.category open eq.ops category functor natural_transformation variables {ob₁ ob₂ : Type} {C : category ob₁} {D : category ob₂} {F G H : C ⇒ D} definition nt_compose (η : G ⟹ H) (θ : F ⟹ G) : F ⟹ H := natural_transformation.mk (take a, η a ∘ θ a) (take a b f, calc H f ∘ (η a ∘ θ a) = (H f ∘ η a) ∘ θ a : assoc ... = (η b ∘ G f) ∘ θ a : naturality ... = η b ∘ (G f ∘ θ a) : assoc ... = η b ∘ (θ b ∘ F f) : naturality ... = (η b ∘ θ b) ∘ F f : assoc

Human-readable proofs

definition infinite_primes (n : nat) : {p | p ≥ n ∧ prime p} := let m := fact (n + 1) in have m ≥ 1, from le_of_lt_succ (succ_lt_succ (fact_pos _)), have m + 1 ≥ 2, from succ_le_succ this, obtain p `prime p` `p ∣ m + 1`, from sub_prime_and_dvd this, have p ≥ 2, from ge_two_of_prime `prime p`, have p > 0, from lt_of_succ_lt (lt_of_succ_le `p ≥ 2`), have p ≥ n, from by_contradiction (suppose ¬ p ≥ n, have p < n, from lt_of_not_ge this, have p ≤ n + 1, from le_of_lt (lt.step this), have p ∣ m, from dvd_fact `p > 0` this, have p ∣ 1, from dvd_of_dvd_add_right (!add.comm ▸ `p ∣ m + 1`) this, have p ≤ 1, from le_of_dvd zero_lt_one this, absurd (le.trans `2 ≤ p` `p ≤ 1`) dec_trivial), subtype.tag p (and.intro this `prime p`)

Structures

  • Special kind of inductive datatype (only one constructor)
  • Projections are generated automatically
  • "Inheritance"
  • Extensively used to formalize the algebraic hierarchy
  • We can view them as parametric modules
structure has_mul [class] (A : Type) := (mul : A → A → A) structure semigroup [class] (A : Type) extends has_mul A := (mul_assoc : ∀a b c, mul (mul a b) c = mul a (mul b c)) ... structure group [class] (A : Type) extends monoid A, has_inv A := (mul_left_inv : ∀a, mul (inv a) a = one)

Sylow theorem

variables {A : Type} [ambA : group A] [finA : fintype A] [deceqA : decidable_eq A] include ambA deceqA finA theorem cauchy_theorem : ∀ p, prime p → p ∣ card(A) → ∃ g : A, order(g) = p theorem first_sylow_theorem : ∀ p, prime p → ∀ n, p^n ∣ card(A) → ∃ (H : finset A) (sg : is_finsubg H), card(H) = p^n

Category Theory

theorem yoneda_embedding (C : Precategory) : C ⇒ set ^c Cᵒᵖ theorem contravariant_yoneda_embedding (C : Precategory) : Cᵒᵖ ⇒ set ^c C

Future work

  • Auto tactic based on equational reasoning, matching, heuristic instantiation, …
  • Decision procedures for arithmetic
  • Efficient evaluator
  • Better support for proof by reflection
  • Better libraries (ongoing work)
  • Machine learning

Thank you