The Lean Theorem Prover
Leonardo de Moura (Microsoft Research),
Soonho Kong (CMU), Jeremy Avigad (CMU),
Floris van Doorn (CMU), Jakob von Raumer (KIT),
Rob Lewis (CMU), Haitao Zhang,
Daniel Selsam (Stanford)
CICM, 2015/07/09
http://leanprover.github.io
Many thanks to
- Cody Roux
- Georges Gonthier
- Grant Passmore
- Nikhil Swamy
- Assia Mahboubi
- Bas Spitters
- Steve Awodey
- Ulrik Buchholtz
- Tom Ball
- Parikshit Khanna
Introduction: Lean
- New open source theorem prover
- Platform for
- Software verification & development
- Formalized mathematics
- Education (mathematics, logic, computer science)
- Synthesis (proofs & programs)
- de Bruijn's Principle: small trusted kernel
- Expressive logic
- Partial constructions: automation fills the "holes"
Introduction: Lean
- It is an ongoing and long long term effort
- At CMU, it is already being used for formalizing
- Homotopy Type Theory
- Category Theory
- Algebraic Hierarchy
- Nonabelian Algebraic Topology
- Number Theory
- Interactive theory proving course at CMU
- Haitao Zhang is formalizing Group Theory
Main Goal
Lean aims to bring two worlds together
- An interactive theorem prover with powerful automation
- An automated reasoning tool that
- produces (detailed) proofs,
- has a rich language,
- can be used interactively, and
- is built on a verified mathematical library
Secondary Goals
- Minimalist and high-performace kernel
- Experiment with different flavors of type theory
- Proof irrelevant vs Proof relevant
- Impredicative vs Predicative
- Higher Inductive Types
- Quotient Types
- Observational Type Theory
- Education
- Interactive courses
- Proving should be as easy as programming
- Have Fun
Software verification and
Formalized Mathematics
- Some projects at Microsoft Research
- Disclaimer: this projects were developed before Lean existed
- They used Boogie/Z3 and Coq.
Software verification and
Formalized Mathematics
- Similar problems
- Proof stability
- Libraries are big
- Scalability issues
- Finding existing functions/theorems
- Common problems in software engineering:
- Every attempt to create a single unified language failed (ADA?)
- We keep reimplementing the same libraries over and over again
- Mixing libraries from different languages is usually a mess
- Bit rotting
- These problems also affect formalized mathematics
What is new?
- Poweful elaboration engine that can handle
- Higher-order unification
- Definitional reductions
- Coercions
- Ad-hoc polymorphism (aka overloading)
- Type classes
- Tactics
"By relieving the brain of all unnecessary work, a good notation sets it free to concentrate on more advanced problems, and in effect increases the mental power of the race." – A. N. Whitehead
What is new?
- Poweful elaboration engine that can handle
- Small trusted kernel
- It does not contain
- Termination checker
- Fixpoint operators
- Pattern matching
- Module management
- It does not contain
What is new?
- Poweful elaboration engine that can handle
- Small trusted kernel
- Multi-core support
- Process theorems in parallel
- Execute/try tactics (automation) in parallel
What is new?
- Poweful elaboration engine that can handle
- Small trusted kernel
- Multi-core support
- Fast incremental compilation
What is new?
- Poweful elaboration engine that can handle
- Small trusted kernel
- Multi-core support
- Fast incremental compilation
- Support for mixed declarative and tactic proof style
Dependent Type Theory
- Before we started Lean, we have studied different theorem provers: ACL2, Agda, Automath, Coq, HOL (family), Isabelle, Mizar, PVS
- Dependent type theory is really beautiful
- Some advantages
- Bultin computational interpretation
- Same data-structure for representing proofs and terms
- Reduce code duplication, example:
- We implemented a compiler for Haskell-like recursive equations, we can use it to construct proofs by induction
- Mathematical structures (such as Groups and Rings) are first-class citizens
- Some references
- In praise of dependent types (Mike Shulman)
- Type inference in mathematics (Jeremy Avigad)
Dependent Type Theory
- Constants
- Function applications
- Lambda abstractions
- Function spaces
Dependent Type Theory
- What is the type of
nat?
- What is the type of
Type?
Is Lean inconsistent? NO
- Lean has a noncumulative universe hierarchy
- Supports universe polymorphism
- In ordinary situations you can ignore the universe parameters and simply write
Type, leaving the "universe management" to Lean
Propositions as types
- Propositions are types
- The inhabitants/elements of a proposition
Pare the proofs ofP Propis the type of all propositions
Architecture
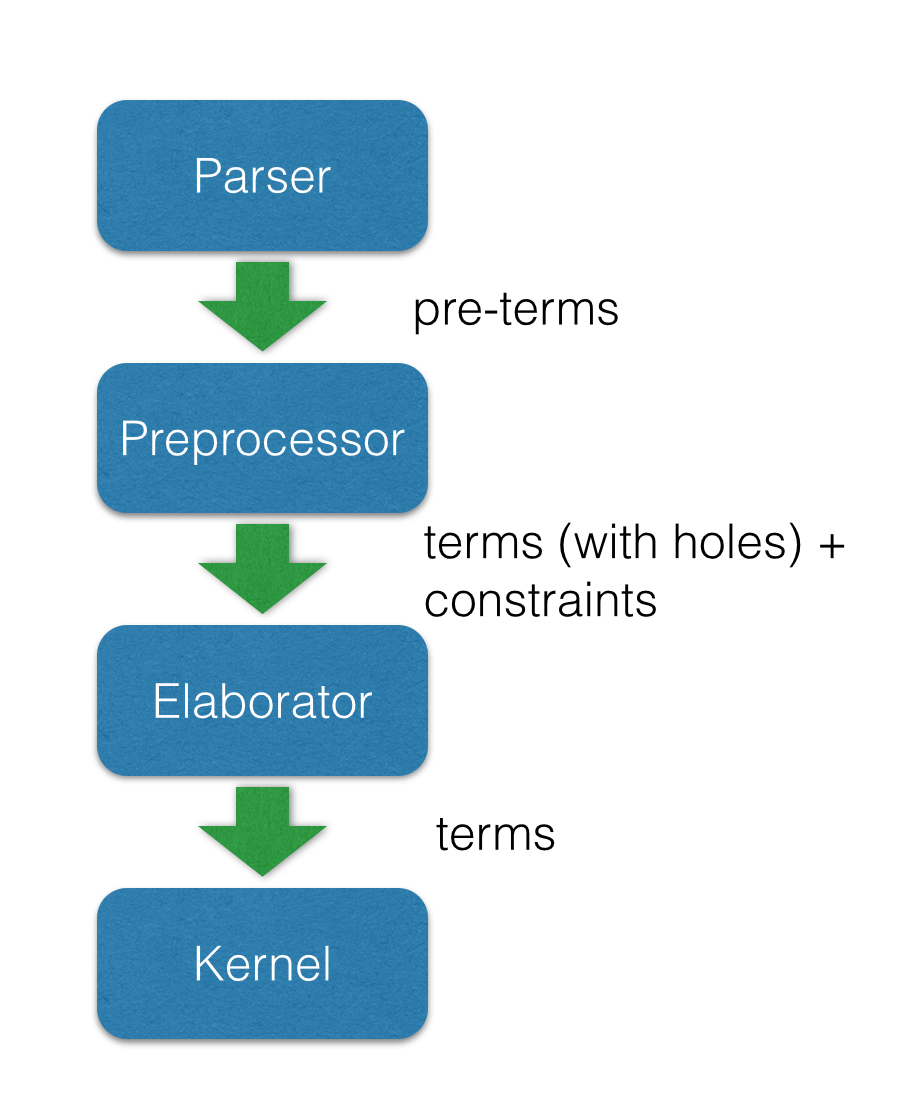
Architecture
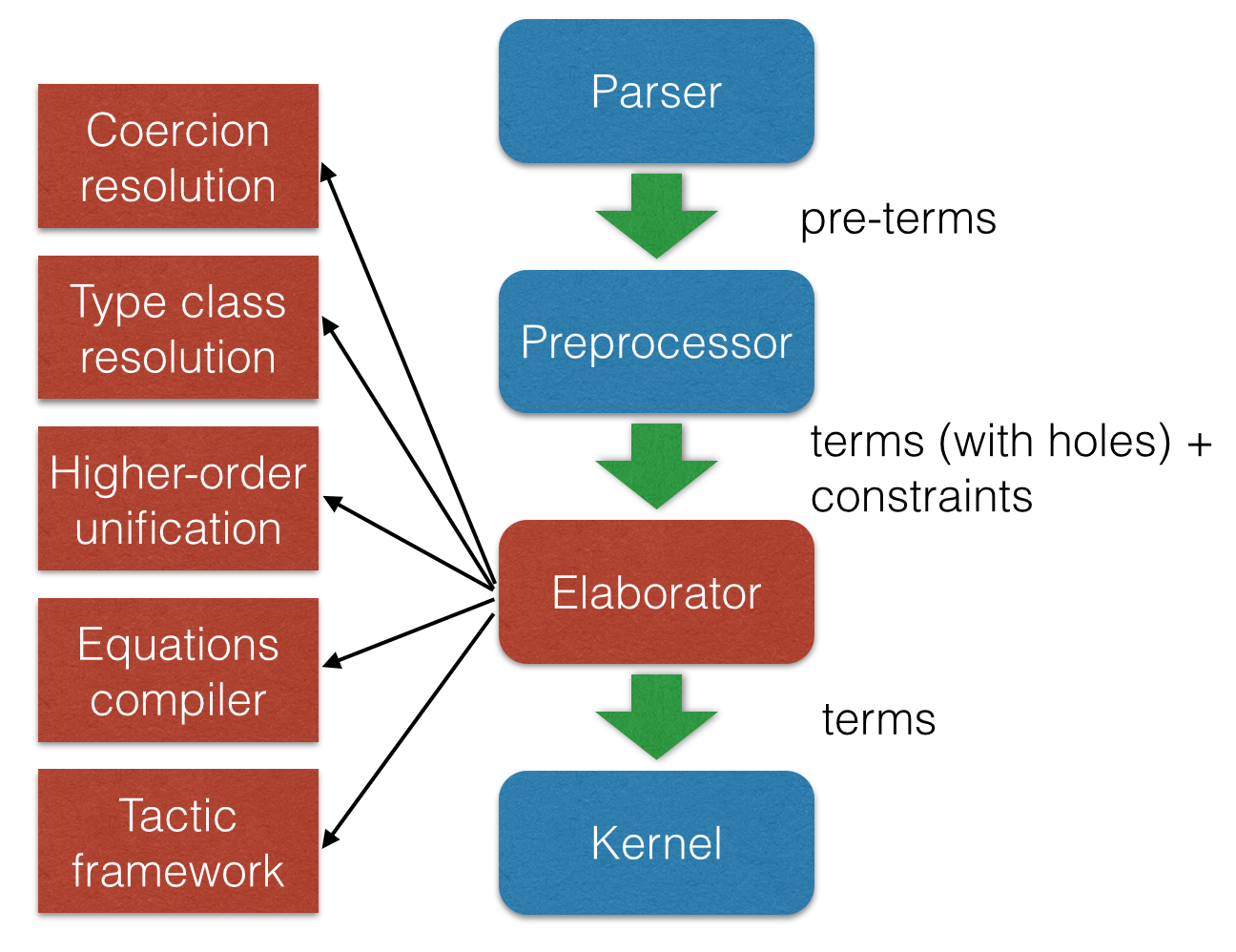
Architecture
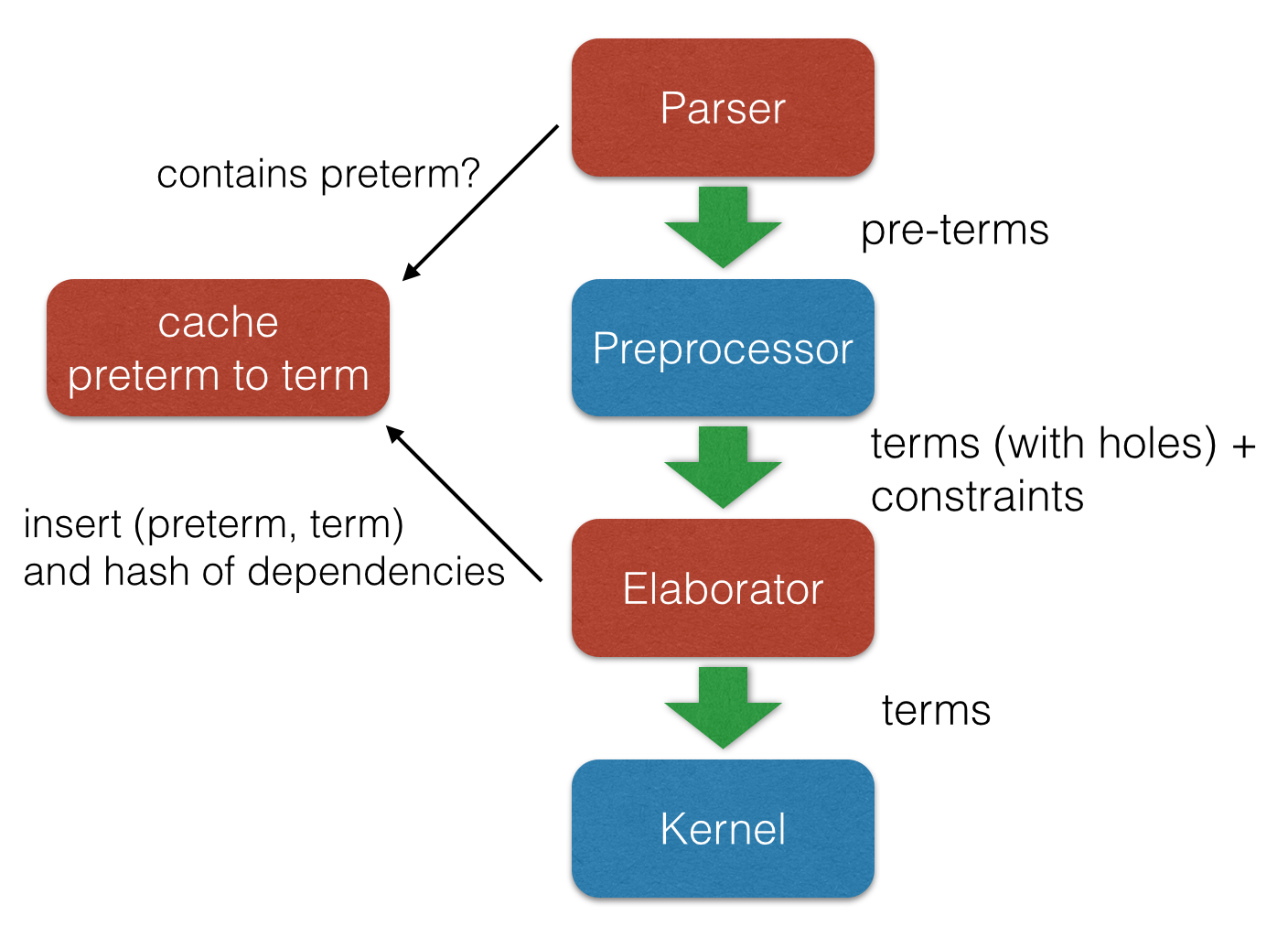
Kernel
- Kernel is implemented in two layers for easy customization
- 1st layer, dependent lambda calculus + options:
- Proof irrelevance
- Impredicative Prop
Π (x : nat), x = x -- is a Proposition ∀ (x : nat), x = x -- Alternative notation - 2nd layer: Inductive families, Quotient types, HITs

Two official libraries
- Standard
- Proof irrelevant and impredicative Prop
- Smooth transition to classical logic
- Inductive Families
- Quotient Types
- HoTT
- Proof relevant and no impredicative Prop
- Univalence axiom
- Inductive Families
- HIT
- Easy to implement experimental versions, Example: Steve Awodey asked for proof relevant and impredicative universe
Agnostic Mathematics
- Support constructive and classical mathematics
- Constructive results are more informative
- Computation is important to mathematics
- Core parts of the standard library are constructive
- Separation of concerns:
- Methods to write computer programs
- Freedom to use a nonconstructive theories and methods to reason about them
Agnostic Mathematics
- Semi constructive axioms:
- Function extensionality
- Proposition extensionality
- Quotient types (implies function extensionality)
- Acceptable classical axiom: proof irrelevant excluded middle
- Anti constructive: Hilbert's choice (aka magic)
- consequence: all propositions are decidable
Freedom to trust
- Option: type check imported modules.
- Macros: semantic attachments for speeding up type checking and evaluation.
- Macros can be eliminated (expanded into pure Lean code).
- Each macro provides a function for computing the type and evaluating an instance.
- Each macro can be assigned a trust level.
- Many applications: interface with the GNU multiprecision arithmetic (GMP) library.
Freedom to trust
- Relaxed mode
- Trust the imported modules have not been tampered
- Trust all macros
- Paranoid mode
- Retype check all imported modules (someone may have changed the binaries)
- Expand all macros (the developers may have made mistakes, GMP may be buggy)
- Stronger guarantee Retype check everything using Lean reference type checker
- Daniel Selsam is implementing a reference type checker in Haskell
Exporting libraries
- All Lean files can be exported in a very simple format
- Documentation is available on github
- Communicate with other tools
- Interface with the Lean reference type checker
Inductive families
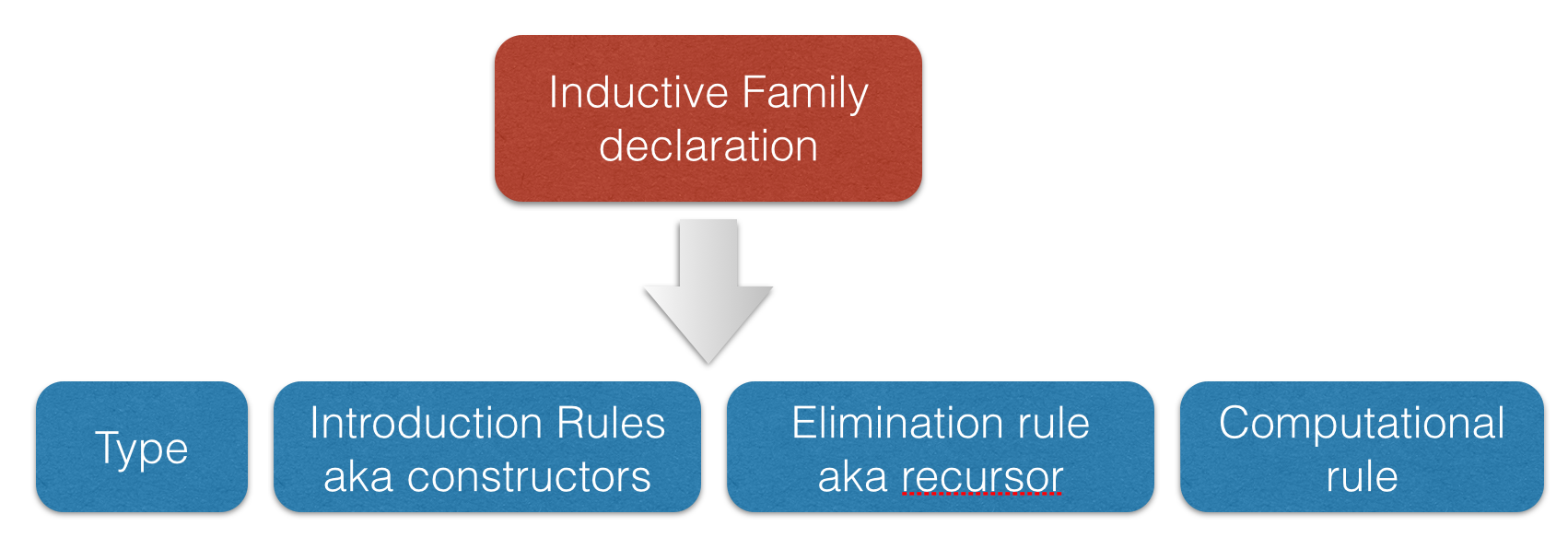
Inductive families
Inductive families
Inductive families
- It is possible to construct a substantial edifice of mathematics based on nothing more than the type universes, function spaces, and inductive types; everything else follows from those.
Implicit arguments
- Curly braces indicate that argument should be inferred rather than entered explicitly.
Implicit arguments
- Elaborator uses higher-order unification.
Recursive equations
- Recursors are inconvenient to use.
- Compiler from recursive equations to recursors.
- Two compilation strategies: structural and well-founded recursion
Recursive equations
- Proofs by induction
Recursive equations
- Dependent pattern matching
Definitional Reductions
- Elaborator must respect the computational interpretation of terms
Coercions
- In Lean, we can associate attributes to definitions.
- Coercion is one of the available attributes.
Namespaces
- We can group definitions, metadata (e.g., notation declarations and attributes) into namespaces.
- We can open namespaces
Ad-hoc polymorphism
- We can use namespaces to avoid unwanted ambiguity.
- We can override overloading
Human-readable proofs
Type classes
- Synthesis procedure based on lambda-Prolog
- Big picture
- Mark some inductive families as classes
- Mark some definitions as (generators of) instances
- Indicate that some implicit arguments must be synthesized using type classes
- Instances are treated as Horn clauses
Inhabited Type Class
Decidable Type Class
- An element of
Propis said to be
decidable if we can decide whether it is true or false.
- Having an element
t : decidable pis stronger than having an elementt : p ∨ ¬p - The expression
if c then t else econtains an implicit argument[d : decidable c]. - If Hilbert's choice is imported, then all propositions are decidable (smooth transition to classical reasoning).
Decidable Type Class
Tactics
- Automation such as rewrite engined, simplifiers and decision procedures are integrated into the system as tactics.
- A placeholder/hole can be viewed as a goal
- A proof state is a sequence of goals, substitution (already solved holes), and postponed constraints.
- A tactic is a function from proof state to a lazy stream of proof states (very similar to Isabelle).
- Tacticals are tactic combinadors: andthen, orelse, par, …
Tactics
- We can switch to tactic mode using begin … end or by …
Structures
- Special kind of inductive datatype (only one constructor)
- Projections are generated automatically
- "Inheritance"
- Extensively used to formalize the algebraic hierarchy
- We can view them as parametric modules
Structures
Structures (additional instances)
Structures (concrete instances)
- Is
intaadd_group? Yes
Sylow theorem
Bundled structures
Future work
- Auto tactic based on equational reasoning, matching, heuristic instantiation, …
- Decision procedures for arithmetic
- Efficient evaluator
- Better support for proof by reflection
- Better libraries (ongoing work)
- Machine learning (ask Daniel)
Thank you
- Website: http://leanprover.github.io/
- Source code: https://github.com/leanprover/lean
- Theorem proving in Lean: https://leanprover.github.io/tutorial/index.html