Lean 4.10.0
We're happy to announce that Lean 4.10.0 has been released!
As usual, this release includes a number of improvements to Lean's internals that improve performance, predictability, and proof automation.
Lean's support for incrementally checking proofs has been improved, the language server is more robust, there were improvements to the split, simp, and rw tactics, and the details of the behavior of def, example, and theorem have been made more consistent with each other.
For a complete accounting, please refer to the release notes; read on for some highlights!
Lake: Reservoir Require
Reservoir, the Lean package database, is now natively supported by Lake, the Lean build tool. Starting in Lean 4.10, a TOML package configuration may write
[[require]] name = "batteries" scope = "leanprover-community"
instead of
[[require]] name = "batteries" git = "https://github.com/leanprover-community/batteries" rev = "main"
and a Lean package configuration may write
require "leanprover-community" / "batteries"
instead of
require batteries from git "https://github.com/leanprover-community/batteries" @ "main"
Retrieving packages through Reservoir instead of directly from Git packages has a number of advantages:
-
Reservoir specifies metadata such as the default branch name, so build configurations don't need to configure them manually unless overriding a default.
-
Lake supports alternative registries and will someday support features like Cargo's source replacement, allowing transitively-depended-upon packages to be overridden by individuals or teams.
-
Organizations with compliance and security requirements or with large existing codebases that impose requirements on integration can provide package registries that enable Lean to be a part of their existing development practices.
-
Packages may change their development or hosting practices without breaking all downstream dependencies.
The scope (e.g., "leanprover-community") is used to disambiguate packages with the same name.
In Reservoir, it's the name of the user or organization who owns the package.
Debugging Options
Trustworthy verification is a major reason to use Lean: the fact that all proofs are verified using a small kernel (and can be re-verified using independent external implementations of the kernel's logic) means that we can be very confident in our proofs. However, checking proofs takes time, and large refactorings that require many changes to a Lean module may be slowed down by repeatedly rechecking proofs. Two new configuration options make it easier to refactor large files by temporarily disabling Lean's proof checking features.
The first, debug.byAsSorry, replaces each tactic script with sorry, which causes Lean to immediately accept the proof.
Because this uses an axiom, the fact that the proof was not really checked is recorded and Lean issues a warning.
When this option is enabled, tactic scripts are never run.
The second, debug.skipKernelTC, disables Lean's kernel.
The kernel would normally check the output of the tactic scripts to ensure that the resulting proof terms are valid.
When debug.skipKernelTC is true, this step does not occur.
Using this option makes Lean unsound, because a buggy tactic could generate an invalid term without an error occurring.
However, there are some Lean files in which kernel execution is a substantial portion of the time take to check a proof, so temporarily disabling it while still running tactics can make it easier to conduct large changes.
It's important that the option be disabled again.
Displaying Large Terms
As Lean is used to tackle larger and larger problems, we need to continually eliminate bottlenecks in the implementation.
Showing extremely large terms in the Lean InfoView can lead to UI slowdowns or even internal stack overflows in the code that converts the terms to JSON to be sent to LSP clients.
Lean 4.6 introduced the option pp.deepTerms, which cuts off pretty-printing of terms at a given nesting depth.
In Lean 4.10, this option is false by default, so deep terms will be cut off after 50 levels of nesting unless users specify otherwise.
However, some terms are very wide without being particularly deep.
These terms would not trigger the cutoff, but they could still lead to performance problems or crashes.
In Lean 4.10, a new option pp.maxSteps sets an upper bound on the overall size of the output by limiting the number of expression nodes that can be shown.
When this count has been exceeded, subterms are replaced by ellipses, and hovers in the InfoView can still be used to explore them.
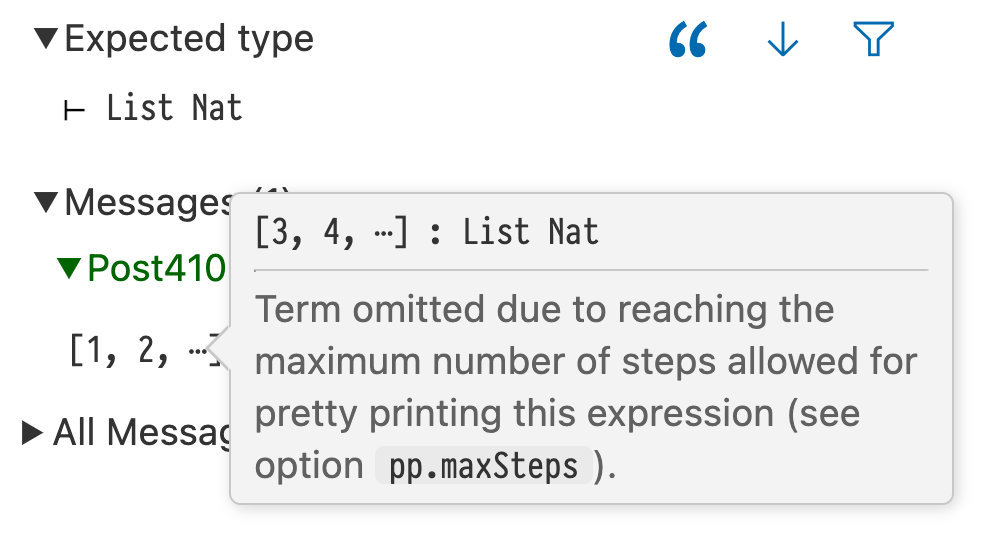
Setting pp.maxSteps to a very small value demonstrates the replacement of terms by ellipses:
set_option pp.maxSteps 4
#reduce [1,2,3,4][1, 2, ⋯]
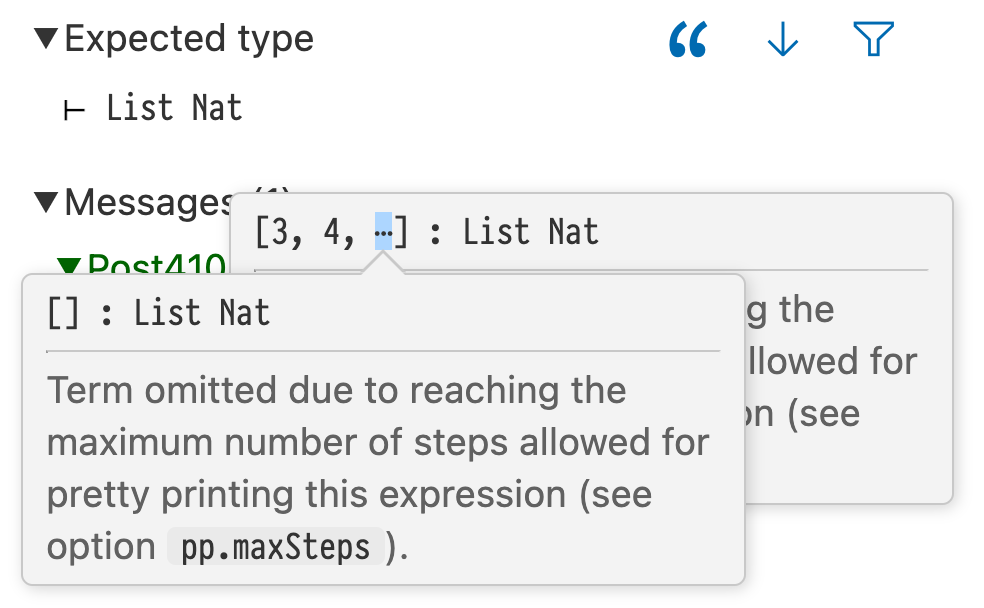
In the Lean InfoView, hovering the mouse over the ellipses reveals the suppressed term, and further hovers can reveal more of it:
Hovering the mouse over the ellipses reveals the hidden term [3, 4, ⋯]
Hovering the mouse over the ellipses in the hover reveals the hidden term []
Outside the core language implementation, we have also put significant effort into the performance of the InfoView in Lean's VS Code plugin, typically resulting in an order of magnitude speedup.
GetElem Split
In Lean, the array index notation xs[i] is syntactic sugar for a call to GetElem.getElem, where the type of indices i and the type of elements is determined by the instance of the GetElem type class.
Additionally, GetElem specifies a relation that determines whether a given index is valid.
For arrays, the index type is Nat and the relation specifies that the index is less than the array's size.
The structure type Three contains exactly three elements:
structure Three (α : Type u) where
first : α
second : α
third : α
For its GetElem instance, the valid indices are natural numbers less than three:
instance : GetElem (Three α) Nat α (fun _ n => n < 3) where
getElem xs i _lt3 :=
match i with
| 0 => xs.first
| 1 => xs.second
| 2 => xs.thirddef abc : Three Char := ⟨'a', 'b', 'c'⟩
#eval abc[1]
A separate syntax xs[i]? returns an Option when the index is invalid.
In prior versions of Lean, this required that the validity predicate was decidable.
In practice, the decidability proof that was present behind the scenes led to automation being less reliable than we'd like.
In Lean 4.10, xs[i]? instead desugars to a call to a method getElem? in a new class GetElem? that extends GetElem.
The new getElem? does not require a proof that index validity is decidable, though the class still takes a validity relation as an argument so that it can extend GetElem.
Here's a GetElem? instance for Three:
instance : GetElem? (Three α) Nat α (fun _ n => n < 3) where
getElem? xs i :=
match i with
| 0 => some xs.first
| 1 => some xs.second
| 2 => some xs.third
| _ => none
There is a default instance of GetElem? that uses the decidability of the validity relation, so most existing code should continue to work.
However, implementing GetElem? directly can simplify proofs by removing validity proof objects, and it can make programs faster by replacing two traversals of a data structure (one to decide validity, and another to compute the value) with a single traversal.
Linter for Constructor/Variable Confusion
Datatype constructors are placed in their datatype's namespace. For example, given the declaration
inductive Tree (α : Type u) : Type u where
| leaf : Tree α
| branch : Tree α → α → Tree α → Tree α
the constructors are named Tree.leaf and Tree.branch.
Users who didn't realize this could end up confused, because leaf alone is interpreted as a pattern that matches any value.
In Lean 4.9, this function was accepted:
def reverse : Tree α → Tree α
| leaf => leafExperienced Lean users would be tipped off by the unexpected acceptance of the missing case. In Lean 4.10, there is an explicit warning when a pattern variable has the same name as a zero-argument constructor of the type:
def reverse : Tree α → Tree α
| leaf => leafLocal variable 'leaf' resembles constructor 'Tree.leaf' - write '.leaf' (with a dot) or 'Tree.leaf' to use the constructor. note: this linter can be disabled with `set_option linter.constructorNameAsVariable false`
More Internals in Lean
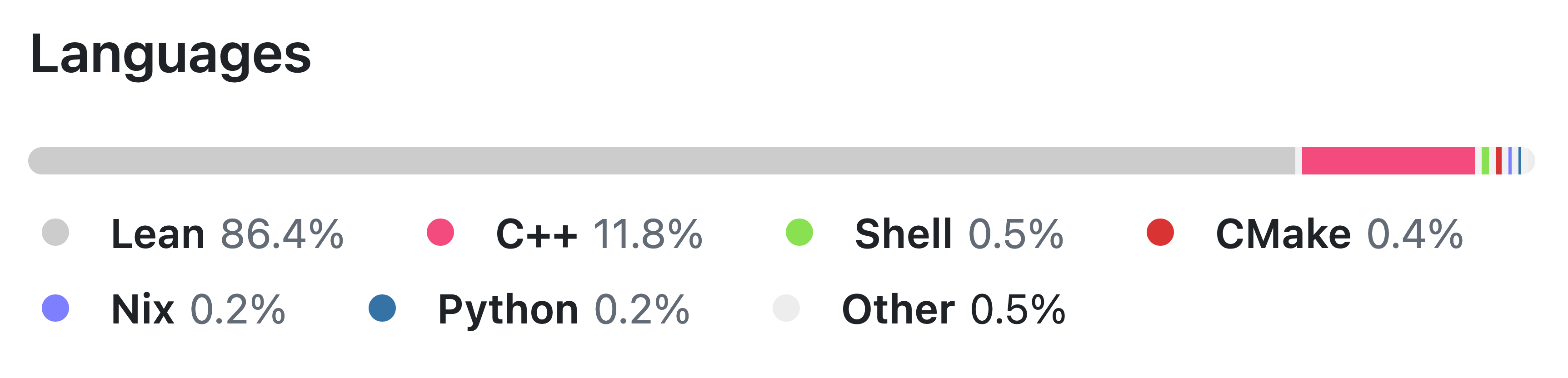
The languages used to implement Lean 4:
- Lean
86.4%
- C++
11.8%
- Others
Less than 1% each of shell, CMake, Nix, and Python
Lean is primarily implemented in Lean, but the runtime system, the trusted kernel, and some parts of the compiler are written in C++.
Lean's equation compiler is responsible for translating pattern matching and recursive definitions into a form accepted by the minimalistic language of the trusted kernel.
This translation proves that the function is total.
The translation process makes use of a number of datatype-specific helpers that capture patterns such as “recursive calls may access any smaller argument” in terms of the datatype's built-in recursion principle, which captures only “recursive calls may access the next structurally-smaller argument.”
In Lean 4.10, the code that generates these helpers, with names such as T.below, T.recOn and T.brecOn, is now implemented in Lean, making the codebase easier to navigate, understand, and maintain.
BEq Argument Order Standardization
In Lean 4.10, we've adopted the convention from Mathlib and Batteries that the arguments to the Boolean equality operator == should always place the “more variable” argument on the left-hand side.
Consistent code style is important in all languages, but it's even more important in Lean because it makes verification easier.
In particular, == is not necessarily symmetric, so a == b may not imply b == a.
Combining theorems and programs that make use of both argument orders imposes extra unnecessary proof obligations.
We encourage the entire Lean community to adopt this convention, so that our growing ecosystem of libraries can be used together without unnecessary friction.
Instead of writing (x == ·), please write (· == x).
Instead of writing:
def fives (xs : List Nat) : List Nat := xs.filter (5 == ·)please write:
def fives (xs : List Nat) : List Nat := xs.filter (· == 5)
In the following function, x remains constant through the recursive calls, while the head of the list y changes, so the comparison is written y == x:
def allThatEqual [BEq α] (x : α) : List α → List α
| [] => []
| y :: ys =>
if y == x then y :: allThatEqual x ys
else allThatEqual x ysReduction Command Configuration
The #reduce command performs all possible reductions in a term, printing the normal form.
When terms contain embedded types or proofs, such as the proof in a Fin n that the natural number is less than n, #reduce can spend a lot of time computing proof objects that may not be interesting.
Reducing proofs may even exceed resource bounds such as the maximum recursion depth. In Lean 4.9, reducing even very simple bitvector expressions can require too many recursive calls:
def seventeen : BitVec 32 := 17
#reduce seventeenmaximum recursion depth has been reached use `set_option maxRecDepth <num>` to increase limit use `set_option diagnostics true` to get diagnostic information
This is because a bitvector of width w is represented as a Nat paired with a proof that it is less than 2^{w}, and the proof may use induction on the upper bound.
In Lean 4.10, the #reduce command no longer performs reduction in types and proofs by default:
def seventeen : BitVec 32 := 17
#reduce seventeen{ toFin := ⟨17, ⋯⟩ }
The configuration options (proofs := true) and (types := true) can be used to re-enable full reduction:
#reduce (proofs := true) seventeenmaximum recursion depth has been reached use `set_option maxRecDepth <num>` to increase limit use `set_option diagnostics true` to get diagnostic information
Breaking Changes
-
String.csizeandChar.utf8Sizehave been unified under the nameChar.utf8Size. -
Library lemmas now follow the “most variable argument first” convention, as described above.
-
The
simpnormal forms for indexing intoListandArrayarexs[n]andxs[n]?, rather than calls to functions likeList.get. Some proofs may require modifications. -
Sometimes terms created via a sequence of unifications will be more eta reduced than before and proofs will require adaptation (see #4387 for more details).
-
As described above, the
GetElemclass has been split into two. Please see the docstrings forGetElemandGetElem?for more information.