Lean 4.8.0

David Thrane ChristiansenSebastian Ullrich

2024-06-01

Release Announcements

Lean 4.8.0 has been released!

Version 4.8.0 is a very big release, containing more than 370 separate improvements. There is no way for a single post to do justice to all of the hard work that has been put into this release. Many of the improvements have served to make Lean faster and more robust, but will be only visible because the whole system feels snappier and reliable. On the other hand, there were also a large number of directly visible enhancements—read on for some highlights!

For a complete accounting of the updates in Lean 4.8.0, please refer to the release notes.

Standard Library

In the past, Lean had a community-developed standard library, maintained separately from the compiler. This library provided not only datatypes and functions, but also tactics, language features like #guard_msgs, linters, and even interactive features such as code actions.

However, an externally-developed standard library comes with a number of drawbacks:

It is difficult to fully integrate features from the library with the rest of the language. For example, when Lean 4.7 moved the omega tactic into Lean itself, it became possible to automatically check that array accesses were in-bounds and to use it for automatic termination arguments.
Features that require tight coordination between compiler improvements and library improvements are much more difficult to implement, because they need to be coordinated across multiple repositories and maintainer teams.
Users are burdened with explicitly tracking their dependency on the standard library in their build system, and some users may not know to use it.

We made the decision to include the standard library as part of Lean itself. Lean 4.7 upstreamed many of the most important, mature parts of the community standard library into the compiler, making them available out of the box for everyone. The community library, now intended for extra contributions that are not part of Lean itself, has been renamed and moved to leanprover-community/batteries, so please update your Lakefiles to point at the new location.

Termination Checking

The termination checker now recognizes more complex patterns of recursive calls, so fewer termination_by clauses are needed. In particular, the common idiom of counting up to a bound rather than down towards zero is now recognized automatically, as in Array.count, which counts the elements of an array that satisfy some Boolean predicate p:

def Array.count (p : α → Bool) (array : Array α) : Nat :=
  let rec go (acc : Nat) (i : Nat) :=
    if h : i < array.size then
      if p array[i] then go (acc + 1) (i + 1)
      else go acc (i + 1)
    else acc
  go 0 0

Functional Induction

Functional induction makes it much easier to write proofs about recursive functions that are not structurally recursive. Typically, proofs about recursive functions must follow the structure of the functions' recursive calls. Structural recursion matches inductive arguments: base cases of the recursion correspond to base cases for the argument, and recursive calls correspond to appeals to an induction hypothesis.

However, functions defined using other patterns of recursion require proofs that are structured similarly. In earlier versions of Lean, these proofs could be written as recursive functions, but Lean 4.8 includes support for functional induction, where recursive functions provide the code that the induction tactic needs in order to follow the structure of their recursion.

In Lean 4.8, a proof that the count will never exceed the size of the array can be written using the induction tactic directly, using the functional induction principle for the inner loop Array.count.go:

theorem Array.count.go_le_size {array : Array α} :
    acc ≤ i → i ≤ array.size →
    Array.count.go p array acc i ≤ array.size := byα:Type u_1acc:Nati:Natp:α → Boolarray:Array α⊢ acc ≤ i → i ≤ array.size → go p array acc i ≤ array.size
  intro hle1 hle2α:Type u_1acc:Nati:Natp:α → Boolarray:Array αhle1:acc ≤ ihle2:i ≤ array.size⊢ go p array acc i ≤ array.size
  induction acc, i using count.go.induct (p := p) (array := array) with
  | case1 acc i inBounds pTrue ih
  | case2 acc i inBounds pFalse ih =>case2α:Type u_1p:α → Boolarray:Array αacc:Nati:NatinBounds:i < array.sizepFalse:¬p array[i] = trueih:acc ≤ i + 1 → i + 1 ≤ array.size → go p array acc (i + 1) ≤ array.sizehle1:acc ≤ ihle2:i ≤ array.size⊢ go p array acc i ≤ array.size
    unfold gocase2α:Type u_1p:α → Boolarray:Array αacc:Nati:NatinBounds:i < array.sizepFalse:¬p array[i] = trueih:acc ≤ i + 1 → i + 1 ≤ array.size → go p array acc (i + 1) ≤ array.sizehle1:acc ≤ ihle2:i ≤ array.size⊢ (if h : i < array.size then if p array[i] = true then go p array (acc + 1) (i + 1) else go p array acc (i + 1)
  else acc) ≤
  array.size
    simp [*]case2α:Type u_1p:α → Boolarray:Array αacc:Nati:NatinBounds:i < array.sizepFalse:¬p array[i] = trueih:acc ≤ i + 1 → i + 1 ≤ array.size → go p array acc (i + 1) ≤ array.sizehle1:acc ≤ ihle2:i ≤ array.size⊢ go p array acc (i + 1) ≤ array.size
    apply ihcase2.hle1α:Type u_1p:α → Boolarray:Array αacc:Nati:NatinBounds:i < array.sizepFalse:¬p array[i] = trueih:acc ≤ i + 1 → i + 1 ≤ array.size → go p array acc (i + 1) ≤ array.sizehle1:acc ≤ ihle2:i ≤ array.size⊢ acc ≤ i + 1case2.hle2α:Type u_1p:α → Boolarray:Array αacc:Nati:NatinBounds:i < array.sizepFalse:¬p array[i] = trueih:acc ≤ i + 1 → i + 1 ≤ array.size → go p array acc (i + 1) ≤ array.sizehle1:acc ≤ ihle2:i ≤ array.size⊢ i + 1 ≤ array.size <;>case2.hle1α:Type u_1p:α → Boolarray:Array αacc:Nati:NatinBounds:i < array.sizepFalse:¬p array[i] = trueih:acc ≤ i + 1 → i + 1 ≤ array.size → go p array acc (i + 1) ≤ array.sizehle1:acc ≤ ihle2:i ≤ array.size⊢ acc ≤ i + 1case2.hle2α:Type u_1p:α → Boolarray:Array αacc:Nati:NatinBounds:i < array.sizepFalse:¬p array[i] = trueih:acc ≤ i + 1 → i + 1 ≤ array.size → go p array acc (i + 1) ≤ array.sizehle1:acc ≤ ihle2:i ≤ array.size⊢ i + 1 ≤ array.size omegaAll goals completed! 🐙
  | case3 =>case3α:Type u_1p:α → Boolarray:Array αacc✝:Nati✝:Nath✝:¬i✝ < array.sizehle1:acc✝ ≤ i✝hle2:i✝ ≤ array.size⊢ go p array acc✝ i✝ ≤ array.size
    unfold gocase3α:Type u_1p:α → Boolarray:Array αacc✝:Nati✝:Nath✝:¬i✝ < array.sizehle1:acc✝ ≤ i✝hle2:i✝ ≤ array.size⊢ (if h : i✝ < array.size then if p array[i✝] = true then go p array (acc✝ + 1) (i✝ + 1) else go p array acc✝ (i✝ + 1)
  else acc✝) ≤
  array.size
    simp [*]case3α:Type u_1p:α → Boolarray:Array αacc✝:Nati✝:Nath✝:¬i✝ < array.sizehle1:acc✝ ≤ i✝hle2:i✝ ≤ array.size⊢ acc✝ ≤ array.size
    omegaAll goals completed! 🐙

theorem Array.count_le_size {array : Array α} :
    array.count p ≤ array.size := byα:Type u_1p:α → Boolarray:Array α⊢ count p array ≤ array.size
  simp [Array.count]α:Type u_1p:α → Boolarray:Array α⊢ count.go p array 0 0 ≤ array.size
  apply Array.count.go_le_sizeaα:Type u_1p:α → Boolarray:Array α⊢ 0 ≤ 0aα:Type u_1p:α → Boolarray:Array α⊢ 0 ≤ array.size <;>aα:Type u_1p:α → Boolarray:Array α⊢ 0 ≤ 0aα:Type u_1p:α → Boolarray:Array α⊢ 0 ≤ array.size omegaAll goals completed! 🐙

Functional induction is described in more detail in Joachim's recent blog post.

Language Server and IDE Improvements

Completion of module names that can be imported

An indication that one of the imported modules has been modified

Import Completion

Lean now supports completing import declarations when a prefix of a module name has already been typed out. For example, attempting to complete import Init.By will now suggest Init.ByCases, whereas it would not offer any completions in previous Lean version. This makes import completion feel more consistent.

Semantic Token Synchronization

In prior versions of Lean, VS Code would sometimes fail to update its semantic tokens. This led to misleading highlighting in the source file. Now, the Lean language server explicitly invalidates the cache more often, leading to up-to-date highlights.

“Restart File” Diagnostic

The language server now detects when the dependencies of the current file have been modified, informing the user that they may wish to refresh the language server's view of the dependencies with the “Restart File” command, initiating a rebuild. In the past, users had to remember to do this on their own, which could lead to wasted work writing proofs about previous versions of definitions.

Foundations of Incrementality

Lean 4.8.0 contains the foundations of incremental processing within commands. Prior versions of Lean save snapshots after each top-level command, allowing Lean to roll back to a state immediately prior to a user's edit to a file before responding to the edit. This incrementality is useful, but it has limitations: command-level granularity means that tactic proofs must be replayed from scratch, and many DSLs are most naturally embedded as a single Lean command.

In Lean 4.8.0, implementors of Lean elaborators can opt in to saving snapshots of the state of their custom elaboration process, and then resume elaboration with one of these snapshots. This can be used by embedded DSLs to achieve incremental re-use of prior elaboration work, making them more responsive in practice.

Support for incrementality in Lean 4.8 is intended for DSL authors to experiment and provide feedback on the API primitives. We are in the process of adding fine-grained incrementality to Lean's own commands and tactics, and we expect to have initial support for fine-grained incremental processing in Lean 4.9, which will provide visible benefits to all Lean users.

Incremental Elaboration of Verso Documents

DSL and command authors can opt-in to experimental support for incremental elaboration. Previously, Verso documents were elaborated in one big step, but now users can track the progress bar just like in ordinary Lean files.

Lake

TOML Configurations

Lean's build tool, lake, provides the full power of Lean for configuring builds. Sometimes, this is extremely useful, but many projects don't need this power. Power has a cost-the need to use Lean to interpret build instructions made it more difficult to write tools in other languages that process Lean build configurations. Now, the most commonly used project configuration settings are available in a TOML format, so library authors can choose the level of power and control that's appropriate to their needs.

name = "aesop"
defaultTargets = ["Aesop"]
testRunner = "test"

[[require]]
name = "batteries"
git = "https://github.com/leanprover-community/batteries"
rev = "main"

[[lean_lib]]
name = "Aesop"

[[lean_lib]]
name = "AesopTest"
globs = ["AesopTest.+"]
leanOptions = {linter.unusedVariables = false}

[[lean_exe]]
name = "test"
srcDir = "scripts"

Lake configuration files can be translated from Lean to TOML automatically: running lake translate-config toml produces a TOML version of the current configuration. This translation does not preserve comments or non-declarative configuration features, but it can save significant time nonetheless.

Today, not all features are available in TOML files. Thus, if both TOML and Lean configuration files exist, Lake uses the Lean version and issues a warning. We encourage you to use the TOML format if it supports everything you need, and we're working on reducing the need for Lean-based configurations by adding declarative support for more build features.

`lake test`

Lake now supports designating scripts or executables to be test runners, using the @[test_runner] attribute. The new lake test command invokes the test runner. Additionally, the new command lake check-test will exit with code 0 if the package has a test runner, or 1 otherwise.

Progress Reporting

In previous versions of Lean, lake emitted a line of plain text for each task it carried out. When running in a terminal with the right features, lake now produces a progress tracker that updates in-place, only emitting persistent lines of text when there is output such as errors or warnings. Additionally, Lake's tracking of errors in build jobs has been made more robust, and it can continue building in more situations even after encountering errors.

The new --wfail and --iofail options to lake build cause a build to fail if any of the jobs log a warning (--wfail) or produce any output or log information messages (--iofail). Unlike some other build systems, these options do NOT convert these logs into errors, and Lake does not abort jobs on such a log—the build will continue unimpeded, and then report an error when it has completed.

Tactic Improvements

Simplifier

The simplifier tactic simp has seen a number of improvements in Lean 4.8.0. Its documentation has been improved, its internal caching behavior is more robust, its behavior for literals has been made more consistent, and it is more robust in the face of loops. Additionally, the new diagnostics infrastructure makes it much easier to find and fix looping simp lemmas or lemmas that match too often but aren't used, among other performance issues.

`omega`

The omega tactic is a solver for a wide range of linear arithmetic problems, first included by default in Lean 4.7. In Lean 4.8, omega's error messages have been greatly improved and a new canonicalizer makes it work more predictably.

Error Messages

Internally, omega supports reasoning about equalities and inequalities of expressions built up using certain operators. Any subexpressions that fall outside of the theory that omega natively supports are considered atomically, as if they were free variables. In Lean 4.8, omega's error messages list the atoms as well as constraints over these atoms that a counterexample may satisfy—because the atoms are uninterpreted, omega may not be able to see that the constraints may in fact not be satisfiable.

Give f with type Nat → Int, the example:

example : -2 + x + f y < -2 - y := byx:Inty:Nat⊢ -2 + x + f y < -2 - ↑y
  omega could not prove the goal:
a possible counterexample may satisfy the constraints
  a + b + c ≥ 0
  c ≥ 0
where
 a := x
 b := f y
 c := ↑yomegaAll goals completed! 🐙

yields the following message:

omega could not prove the goal:
a possible counterexample may satisfy the constraints
  a + b + c ≥ 0
  c ≥ 0
where
 a := x
 b := f y
 c := ↑y

The where clause at the bottom lists the atoms that omega identified. Seeing the atoms and the constraints can make it easier to diagnose why omega failed to discharge a goal.

Canonicalizer

When omega is deciding whether two subterms of a goal are the same atom, it uses syntactic equality, because checking full definitional equality proved to be too slow in practice. However, this could lead to minor differences in things like terms found by type class synthesis causing omega to treat seemingly-identical terms as different. In Lean 4.8, a fast canonicalization pass is applied prior to atom selection, leading to omega succeeding more often but without slowing down the tactic.

`#guard_msgs` improvements

The #guard_msgs command, used for writing quick inline tests in a file, has gained a number of new features. Whitespace normalization and message sorting make it easier to write tests that are robust and don't fail spuriously, while diff output makes it easier to diagnose the reason why a test is failing.

Whitespace Normalization

Most developers configure their editors to remove trailing whitespace from lines of code automatically. But this can cause problems if the program being tested ends a line of output with a space, because there is no way to include that space in the expected output that does not risk getting deleted automatically. Additionally, long lines of output could interfere with code style warnings about maximum line lengths. Lean 4.8.0 contains new solutions to these problems: #guard_msgs now has new whitespace normalization features as well as a special character (⏎) to protect trailing whitespace.

Normally, #guard_msgs normalized whitespace by converting all newline characters to spaces when comparing to the expected message, to accommodate code style warnings, but now (whitespace := exact) turns off whitespace normalization completely, and (whitespace := lax) collapses all runs of whitespace into a single space, so changes to formatting like indentation will not cause test failures.

Sorting

Because commands may also produce multiple messages in a nondeterministic order, #guard_msgs can also now sort the messages prior to comparison. This feature is off by default, but can be enabled by passing the (ordering := sorted) option.

Diffs

Finally, diagnosing test failures that result from small changes in a relatively large output can be difficult. Starting in Lean 4.8, setting the option guard_msgs.diff to true causes the test failure to contain a diff of the expected and actual messages.

Tree.build constructs a binary tree. Diagnosing test failures that include large trees can be difficult, and it can be tempting to have Lean simply update the expected output with the actual output. For example:

set_option guard_msgs.diff false in
/--
info: Tree.branch
  (Tree.branch
    (Tree.branch
      (Tree.branch (Tree.branch (Tree.leaf 4) 1 (Tree.leaf 2)) 2 (Tree.leaf 2))
      3
      (Tree.leaf 3))
    4
    (Tree.leaf 3))
  5
  (Tree.leaf 3)
-/
❌ Docstring on `#guard_msgs` does not match generated message:

info: Tree.branch
  (Tree.branch
    (Tree.branch
      (Tree.branch (Tree.branch (Tree.leaf 4) 1 (Tree.leaf 2)) 2 (Tree.leaf 2))
      3
      (Tree.leaf 2))
    4
    (Tree.leaf 2))
  5
  (Tree.leaf 2)#guard_msgs in
Tree.branch
  (Tree.branch
    (Tree.branch
      (Tree.branch (Tree.branch (Tree.leaf 4) 1 (Tree.leaf 2)) 2 (Tree.leaf 2))
      3
      (Tree.leaf 2))
    4
    (Tree.leaf 2))
  5
  (Tree.leaf 2)
#eval Tree.build 5 4

fails with:

❌ Docstring on `#guard_msgs` does not match generated message:

info: Tree.branch
  (Tree.branch
    (Tree.branch
      (Tree.branch (Tree.branch (Tree.leaf 4) 1 (Tree.leaf 2)) 2 (Tree.leaf 2))
      3
      (Tree.leaf 2))
    4
    (Tree.leaf 2))
  5
  (Tree.leaf 2)

This can be manually compared to the expected string. With guard_msgs.diff enabled, the test still fails:

set_option guard_msgs.diff true in
/--
info: Tree.branch
  (Tree.branch
    (Tree.branch
      (Tree.branch (Tree.branch (Tree.leaf 4) 1 (Tree.leaf 2)) 2 (Tree.leaf 2))
      3
      (Tree.leaf 3))
    4
    (Tree.leaf 3))
  5
  (Tree.leaf 3)
-/
❌ Docstring on `#guard_msgs` does not match generated message:

  info: Tree.branch
    (Tree.branch
      (Tree.branch
        (Tree.branch (Tree.branch (Tree.leaf 4) 1 (Tree.leaf 2)) 2 (Tree.leaf 2))
        3
-       (Tree.leaf 3))
+       (Tree.leaf 2))
      4
-     (Tree.leaf 3))
+     (Tree.leaf 2))
    5
-   (Tree.leaf 3)
+   (Tree.leaf 2)
#guard_msgs in
Tree.branch
  (Tree.branch
    (Tree.branch
      (Tree.branch (Tree.branch (Tree.leaf 4) 1 (Tree.leaf 2)) 2 (Tree.leaf 2))
      3
      (Tree.leaf 2))
    4
    (Tree.leaf 2))
  5
  (Tree.leaf 2)
#eval Tree.build 5 4

However, the error message includes the lines that differ:

❌ Docstring on `#guard_msgs` does not match generated message:

  info: Tree.branch
    (Tree.branch
      (Tree.branch
        (Tree.branch (Tree.branch (Tree.leaf 4) 1 (Tree.leaf 2)) 2 (Tree.leaf 2))
        3
-       (Tree.leaf 3))
+       (Tree.leaf 2))
      4
-     (Tree.leaf 3))
+     (Tree.leaf 2))
    5
-   (Tree.leaf 3)
+   (Tree.leaf 2)

This option is presently off by default while we experiment with it and refine the user experience, but we do plan to enable it by default in a future release. Please test it out and let us know what works well and what needs improvement.

More Performance Diagnostic Tools

For advanced users who would like to understand how to improve the elaboration time of their Lean programs and proofs, Lean 4.8.0 provides two new tools: a central option that controls the display of a number of internal counters, and support for exporting profiler data to the Firefox Profiler.

Diagnostics Counters

If a program or proof is taking too long to elaborate, use set_option diagnostics true to enable the tracking and printing of a number of counters across various Lean subsystems. Values that exceed the threshold set in diagnostics.threshold are reported. For type class synthesis, this option currently tracks unfoldings per declaration and uses per instance, and for simp, it tracks the number of times each simp theorem is used and the number of times it is tried. This information is especially helpful for finding type class instances or simp theorems that slow down instance synthesis or simplification. More metrics may be added in the future.

In this example, two simp lemmas induce a loop:

@[simp]
theorem one_plus_eq_plus_one : 1 + n = n + 1 := byn:Nat⊢ 1 + n = n + 1 apply Nat.add_commAll goals completed! 🐙

@[simp]
theorem plus_one_eq_one_plus : n + 1 = 1 + n := byn:Nat⊢ n + 1 = 1 + n apply Nat.add_commAll goals completed! 🐙

theorem looping : k + 1 > 0 := byk:Nat⊢ k + 1 > 0 tactic 'simp' failed, nested error:
maximum recursion depth has been reached
use `set_option maxRecDepth <num>` to increase limit
use `set_option diagnostics true` to get diagnostic informationsimpk:Nat⊢ k + 1 > 0

This leads to simp looping until it reaches its maximum recursion depth:

tactic 'simp' failed, nested error:
maximum recursion depth has been reached
use `set_option maxRecDepth <num>` to increase limit
use `set_option diagnostics true` to get diagnostic information

Enabling diagnostics

@[simp]
theorem one_plus_eq_plus_one : 1 + n = n + 1 := byn:Nat⊢ 1 + n = n + 1 apply Nat.add_commAll goals completed! 🐙

@[simp]
theorem plus_one_eq_one_plus : n + 1 = 1 + n := byn:Nat⊢ n + 1 = 1 + n apply Nat.add_commAll goals completed! 🐙

theorem looping : k + 1 > 0 := byk:Nat⊢ k + 1 > 0 tactic 'simp' failed, nested error:
maximum recursion depth has been reached
use `set_option maxRecDepth <num>` to increase limit
use `set_option diagnostics true` to get diagnostic informationsimpk:Nat⊢ k + 1 > 0

This reports the following counters, making the looping simp theorems apparent:

[simp] used theorems (max: 250, num: 2):
    one_plus_eq_plus_one ↦ 250
    plus_one_eq_one_plus ↦ 250
[simp] tried theorems (max: 251, num: 2):
    plus_one_eq_one_plus ↦ 251, succeeded: 250
    one_plus_eq_plus_one ↦ 250, succeeded: 250

Firefox Profiler

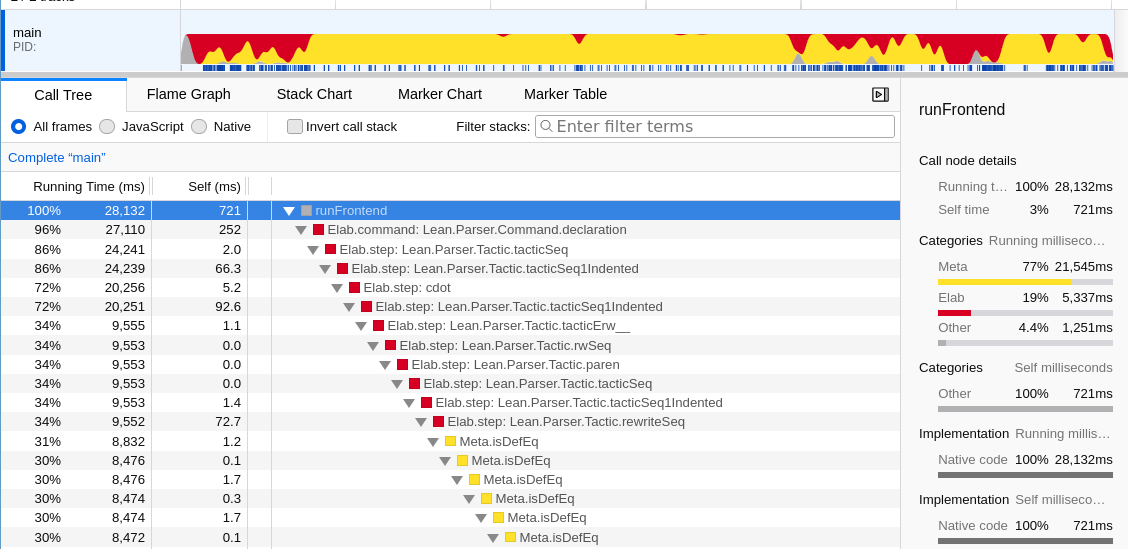
The second tool is an extension of the existing trace.profiler option, which annotates Lean's existing subsystem traces with timing information and automatically unfolds them according to trace.profiler.threshold. The trace profiler can be used to understand time usage by elaboration steps (subterms, tactics, ...) and by Lean subsystems. However, while the produced trace tree can be explored interactively in the Lean Infoview, a textual timeline representation is still bothersome to navigate and comprehend. The new trace.profiler.output sub-option can be used on the command line to instead generate a profile that can be opened in the Firefox Profiler UI.

lake env lean -Dtrace.profiler=true -Dtrace.profiler.output=out.json YourFile.lean

On top of a more powerful tree view that now distinguishes between “running” (inclusive) and “self” (exclusive) time spent at each node, Firefox Profiler provides a linear timeline view that can give an immediate visual impression of bottlenecks in a file, which can further be inspected by hovering over the timeline and focused on a specific point in time in the tree view by clicking. A “flame graph” view that recursively merges sibling nodes with identical labels is also provided.

A profile that shows invoking the call hierarchy feature in the Lean language server, viewed in the Firefox Profiler

Apart from better visualization, Firefox Profiler also supports some transformations of the trace tree that can be helpful for further analyses such as focusing on, merging, or collapsing certain trace classes (labelled "functions") or categories, or inverting the trace tree ("call stack") in order to inspect the most expensive leaf processes.

Finally, two further sub-options can be helpful for some performance investigations:

trace.profiler.useHeartbeats can be used for debugging timeouts by changing the report from wall-clock time to Lean's “heartbeat” metric.
trace.profiler.output.pp exports the full trace node labels for a more detailed profile instead of aggregating per trace class and syntax kind.

Other

Shorter Instance Names

When defining instances of type classes that aren't explicitly named, Lean generates a name internally. This name is based on the class and the types involved. The algorithm used in prior versions of Lean, however, led to some very long names. These names occurred from time to time in error messages, generated API documentation, and other places, and the very long names could cause user interface problems. A new algorithm has been adopted, shortening instance names drastically.

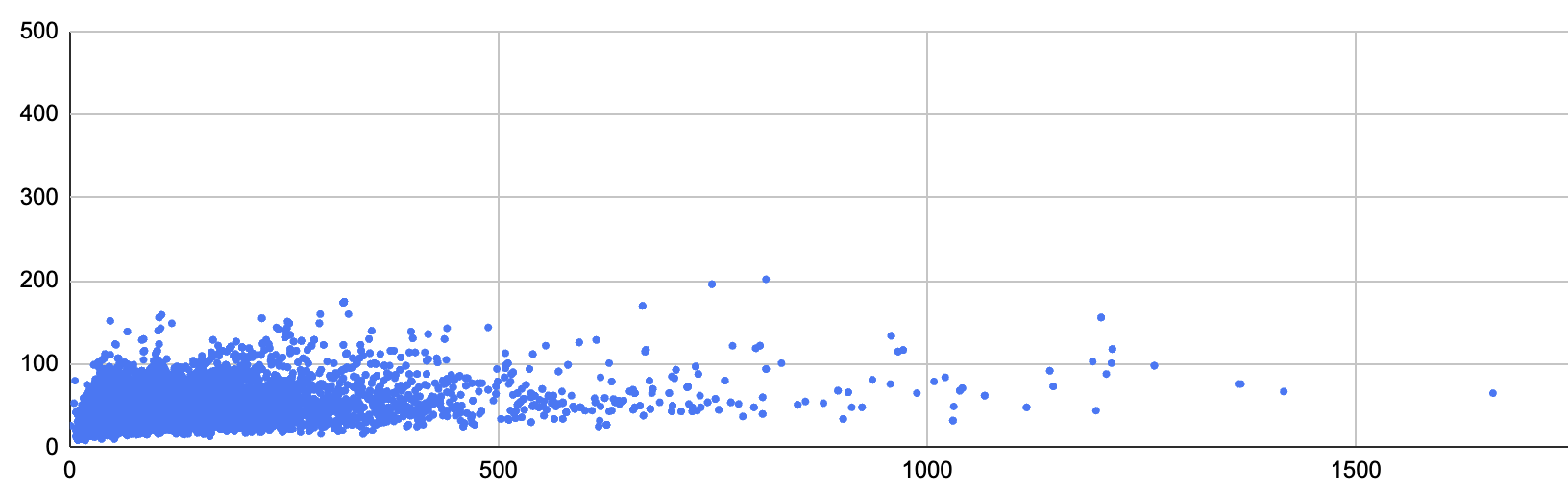
Across Batteries and Mathlib, the median ratio between lengths of new names and of old names is about 72%. With the old algorithm, the longest name was 1660 characters, and now the longest name is 202 characters. The new algorithm's 95th percentile name length is 67 characters, versus 278 for the old algorithm. While the new algorithm produces names that are 1.2% less unique, it avoids cross-project collisions by adding a module-based suffix when it does not refer to declarations from the same "project" (modules that share the same root). This plot shows the name lengths in Lean 4.7 (x-axis) and vs 4.8 (y-axis):

A plot showing the lengths of automatically generated instance names in Lean 4.7 (x-axis) and Lean 4.8 (y-axis).

Aside from shorter names in proof goals, error messages, and generated API references, most users shouldn't notice any changes. However, code that relies on the particular names chosen by the algorithm will need to be updated.

Pretty-Printer Improvements

Printing with Anonymous Constructors

Tagging a structure type with the pp_anonymous_constructor attribute causes the Lean to use the angle-bracket syntax for anonymous constructors when displaying instances of the structure. For example, this structure uses Lean's default pretty-printing strategy:

structure Bike where
  wheelCount : Nat := 2
  hasBox : Bool := false

def commuter : Bike where

def family : Bike where
  wheelCount := 3
  hasBox := true

def commuter : Bike :=
{ wheelCount := 2, hasBox := false }#print commuter
def family : Bike :=
{ wheelCount := 3, hasBox := true }#print family

It displays the two definitions with their field names:

def commuter : Bike :=
{ wheelCount := 2, hasBox := false }

def family : Bike :=
{ wheelCount := 3, hasBox := true }

Adding the attribute to Bike, as in:

@[pp_using_anonymous_constructor]
structure Bike where
  wheelCount : Nat := 2
  hasBox : Bool := false

results in the #print commands instead displaying

def commuter : Bike :=
⟨2, false⟩

and

def family : Bike :=
⟨3, true⟩

Field Notation

In previous versions of Lean, structure projections could be printed using field notation. In Lean 4.8, this feature has been generalized so that any function in a type's namespace is eligible to be printed using field notation. This change makes Lean's output more closely resemble idiomatic Lean code. Field notation is now controlled by the options pp.fieldNotation (which replaces pp.structureProjections) and pp.fieldNotation.generalized, which enables field notation for functions that are not structure field projections. Both now default to true.

In the output of #check below, three.val is used rather than Bounded.val three:

structure Bounded (lo hi : Nat) where
  val : Nat
  lo_le_val : lo ≤ val := by omega
  val_lt_hi : val < hi := by omega

def three : Bounded 2 6 where
  val := 3

three.val : Nat#check three.val

three.val : Nat

In Lean 4.8, field notation is also used by default for Bounded.add1, even though it isn't a field projection:

def Bounded.add1 : Bounded lo hi → Bounded (lo + 1) (hi + 1)
  | {val, ..} => {val := val + 1}

three.add1 : Bounded (2 + 1) (6 + 1)#check three.add1

three.add1 : Bounded (2 + 1) (6 + 1)

This notation is not used for theorems, and it can be disabled on a case-by-case basis by applying the @[pp_nodot] attribute to the function that should not be displayed as a field.

Suppressing Metavariables

During elaboration, Lean represents parts of a term that have not yet been found using metavariables. In Lean's output, these metavariables are denoted ?m.XYZ, where XYZ is a unique number. While these numbers make it possible to connect multiple occurrences of the same unknown value, they are also ephemeral, and very small changes to the program or to Lean's internals can cause different numbers to be assigned. This can make it difficult to maintain tests that involve terms that include metavariables. Lean 4.8 includes the options pp.mvars and pp.mvars.withType that can make messages stable in the face of metavariable renumbering. Setting pp.mvars to false causes Lean to display metavariables as ?_, and setting pp.mvars.withType to true causes Lean to insert a type annotation around each metavariable.

The command

#eval don't know how to synthesize implicit argument
  @none ?m.53180
context:
⊢ Type ?u.53179none

displays numbered metavariables for the unknown type and universe level of the optional value's type:

don't know how to synthesize implicit argument
  @none ?m.53180
context:
⊢ Type ?u.53179

Setting pp.mvars to false removes the internal numbers from the display:

set_option pp.mvars false in
#eval don't know how to synthesize implicit argument
  @none ?_
context:
⊢ Type _none

don't know how to synthesize implicit argument
  @none ?_
context:
⊢ Type _

Additionally setting pp.mvars.withType to true shows the type of each metavariable:

set_option pp.mvars false in
set_option pp.mvars.withType true in
#eval don't know how to synthesize implicit argument
  @none (?_ : Type _)
context:
⊢ Type _none

don't know how to synthesize implicit argument
  @none (?_ : Type _)
context:
⊢ Type _

Induction and Case-Splitting Eliminators

In previous versions of Lean, the @[eliminator] attribute could be used to provide a custom induction principle that would be used by default in the induction and cases tactics. Lean 4.8.0 provides more fine-grained control, replacing this attribute with @[induction_eliminator] and @[cases_eliminator]. These attributes are used to provide eliminators for Nat that show 0 and n + 1 in proof states, rather than the zero and succ constructors. This can also be used to provide an “inductive view” on a type while using a more efficient representation behind the scenes.

Breaking Changes

The following breaking changes may affect Lean users:

theorem statements must be propositions: Lean no longer accepts theorems whose types are not propositions. Please use def to define them.
Lake API updates: Lake's internals have been drastically changed to support the improved tracking of build jobs. Functions like logStep are no longer necessary, and the structure of the API has changed. Nevertheless, we expect that the most user-defined facets and scripts will only need minor changes (if any) to work in the new version.
Lake's nativeFacets setting: The signature of the nativeFacets Lake configuration options has changed from a static Array to a function (shouldExport : Bool) → Array. See its docstring or Lake's README for further details on the changed option.
Windows build changes: Lean is now built as a shared library on Windows, so Lean executables that set supportInterpreter := true are dynamically linked to libleanshared.dll and libInit_shared.dll. Running such executables via lake exe will automatically ensure that these libraries are available, but if they are used in another context, then the libraries must be co-located with the executable or available on $PATH.
Subarray fields renamed: The fields of the Subarray type have been renamed to bring them in line with Lean conventions. The field as has been renamed to array, the field formerly known as h₁ is now named start_le_stop, and h₂ has been renamed to stop_le_array_size.
Removed coercion from String to Name: Prior versions of Lean would automatically apply Name.mkSimple to coerce Strings into Names. However, experience showed that this coercion is not always what's desired. Metaprogram authors who relied on this coercion should insert explicit calls to Name.mkSimple.
Option.toMonad renamed to Option.getM: Additionally, the spurious [Monad m] instance argument was removed.
Naming of equational theorems: Proving that a function terminates can involve significant transformations, sometimes leading to definitions in Lean's core theory that are quite different from their source code. That's why Lean generates equational theorems for definitions that prove that the original defining equations of the function hold, allowing users to reason using the original definition. In Lean 4.8, these equational theorems have been renamed from f._eq_N to f.eq_N (where f is the function in question and N ∈ 1...), and the theorem that relates a defined name to its meaning has been renamed from f._unfold to f.eq_def.
Nested actions cannot be lifted over pure if: Nested actions are monadic actions written in a pure expression context under a do block, surrounded by (← ...). They are equivalent to introducing a fresh let x ← ..., where x is otherwise unused, just before the expression and then referring to x. This could lead to confusing behavior when a non-monadic if-expression had a nested action in only one branch that ended up being lifted over the if and running no matter which branch is selected. Lean no longer lifts nested actions out of pure if-expressions.