Lean 4.6.0

Kim MorrisonDavid Thrane Christiansen
2024-2-29

We're pleased to announce the release of Lean version 4.6.0! This is a big release, with significant improvements made to termination arguments, the simplifier, and the language server. On top of these headlines, there is the usual collection of improvements. The release notes contain more details.

Termination

Lean allows arbitrary recursive functions with the partial keyword, but otherwise functions must pass Lean's termination checker (and only functions passing the termination checker may be unfolded in proofs). In Lean 4.5.0, Lean gained support for automatically proving termination for more recursive definitions. But improved automation can never capture all termination arguments, so it's sometimes necessary to spell out to Lean why a function call does not lead to infinite loops by specifying a decreasing measure.

An explicit termination argument has two components:

  • The measure itself: an expression that is smaller at each recursive call, provided with the termination_by clause

  • A proof that the size of the measure is in fact smaller at each recursive call, provided with the decreasing_by clause

Both aspects have been improved in Lean 4.6.0.

Termination Measures

Prior to Lean 4.6.0, in a mutual block termination_by clauses were collected at the bottom of block. Now they are provided separately at each function definition. This has allowed the syntax to become much simpler. At the sime time, some confusing aspects were made consistent with the rest of Lean.

Instead of repeating the function name and providing parameter names, the parameter names from the signature are automatically in scope:

def findFrom? [BEq α] (needle : α) (haystack : Array α) (start : Nat) : Option Nat :=
  if h : start < haystack.size then
    if haystack[start] == needle then some start
    else findFrom? needle haystack (start + 1)
  else none
termination_by findFrom? needle haystack start => haystack.size - start
termination_by haystack.size - start

When a termination measure uses unnamed arguments, they can still be bound before a => and used in the measure. The names are taken from left to right, and there's no need to write the function's name (or a placeholder for it):

def ackermann : Nat → Nat → Nat
  | 0, m => m + 1
  | n + 1, 0 => ackermann n 1
  | n + 1, m + 1 => ackermann n (ackermann (n + 1) m)
termination_by _ n m => (n, m)
termination_by n m => (n, m)

Termination measures for functions defined using let rec are now located along with the function, rather than together at the bottom of the overall definition:

def find? [BEq α] (needle : α) (haystack : Array α) : Option Nat :=
  let rec go (i : Nat) :=
    if h : i < haystack.size then
      if haystack[i] == needle then some i
      else go (i + 1)
    else none
  termination_by haystack.size - i
  go 0
termination_by go haystack i => haystack.size - i

Likewise, termination measures for functions defined in where-clauses are now placed together with the function:

def find? [BEq α] (needle : α) (haystack : Array α) : Option Nat :=
  go 0
where
  go (i : Nat) :=
    if h : i < haystack.size then
      if haystack[i] == needle then some i
      else go (i + 1)
    else none
  termination_by haystack.size - i
termination_by go haystack i => haystack.size - i

This new syntax is more predictable, less verbose, and it places termination measures closer to the functions.

Termination Arguments

Once a termination measure has been specified, Lean requires a proof that each recursive call decreases the measure. There is a default tactic that works for many common termination proofs, but it is limited to fairly simple patterns of reasoning. The decreasing_by clause is used to specify a proof script that demonstrates that the measure decreases.

Each recursive call in the function corresponds to a proof goal. In prior versions of Lean, the proof script in the decreasing_by clause was run on all of the goals, as if copy-pasted, but this behavior could be inconvenient when each goal requires separate reasoning. This could be worked around by using the error-recovery combinator first, but the results were inelegant.

Starting in Lean 4.6.0, the behavior of decreasing_by is consistent with that of by, with tactics applying to the first goal. The all_goals combinator can be used to apply a tactic to every goal, such as simp_wf, which simplifies termination goals to remove Lean internals. As usual, bullets can be used to structure a proof by focusing on individual goals. For example, this (very pedantic and verbose) termination proof carries out separate reasoning in each goal:

def gcd (n k : Nat) : Nat := if n = 0 then k else if k = 0 then n else if n > k then gcd (n - k) k else gcd n (k - n) termination_by n + k decreasing_by all_goals
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:¬n > k
⊢ n + (k - n) < n + k
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:n > k
⊢ n - k + k < n + k
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:n > k
⊢ n < n + k
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:n > k
⊢ k ≤ n
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:n > k
⊢ n < n + k
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:n > k
⊢ 0 < k
h
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:n > k
⊢ k ≠ 0
All goals completed! 🐙
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:n > k
⊢ k ≤ n
h
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:n > k
⊢ k < n
All goals completed! 🐙
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:¬n > k
⊢ n + (k - n) < n + k
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:¬n > k
⊢ k < n + k
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:¬n > k
⊢ n ≤ k
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:¬n > k
⊢ k < n + k
a._@.Std.Data.Nat.Lemmas._hyg.5450
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:¬n > k
⊢ 0 < n
a.h._@.Std.Data.Nat.Lemmas._hyg.5450
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:¬n > k
⊢ n ≠ 0
All goals completed! 🐙
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:¬n > k
⊢ n ≤ k
a._@.Init.Core._hyg.265
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:¬n > k
⊢ ¬k < n
All goals completed! 🐙

Often, however, all the termination goals can be proven by a more powerful tactic, such as omega. In this case, all_goals is usually the right tool for the job:

def gcd (n k : Nat) : Nat := if n = 0 then k else if k = 0 then n else if n > k then gcd (n - k) k else gcd n (k - n) termination_by n + k decreasing_by all_goals
n:Nat
k:Nat
h✝²:¬n = 0
h✝¹:¬k = 0
h✝:¬n > k
⊢ n + (k - n) < n + k
;
All goals completed! 🐙

Just like termination_by, the decreasing_by clause is now attached to each function definition.

Custom Simplification Procedures

Lean's all-purpose simplification tactic simp gained a powerful new feature: custom simplification procedures, called "simprocs". Typically, simp rewrites a goal according to a collection of simplification lemmas, which are equality proofs. Roughly speaking, if the universally-quantified variables in a simplification lemma can be instantiated such that the left-hand side occurs in the term to be simplified, then it is rewritten to the right-hand side, as long as simp can also prove the side conditions of the lemma. But this approach is not always sufficiently flexible.

Simprocs allow arbitrary Lean code to be used for rewriting of terms using their internal representation as a Lean datatype. While they are trickier to define than ordinary simp lemmas, they enable library authors to provide simplification rules that were impossible to implement as ordinary lemmas, including:

  • Support for reducing numeric literals, which are handled specially by Lean for performance reasons, so 1000 + 2000 simplifies directly to 3000

  • Simplification procedures for custom theories, such as using ring axioms or performing polynomial factorization

  • Simplification using custom simplification strategies. One example in Lean is a simproc for if-then-else-expressions that first tries to simplify the condition. If it simplifies to true, only the then-branch needs to be simplified, and if it simplifies to false, only the else-branch needs to be simplified.

  • Users can write simprocs that interrupt simplification when a specific pattern is found.

For examples, please see the release notes. Even users who do not directly implement their own simprocs will benefit from the improved automation in simp.

Language Server

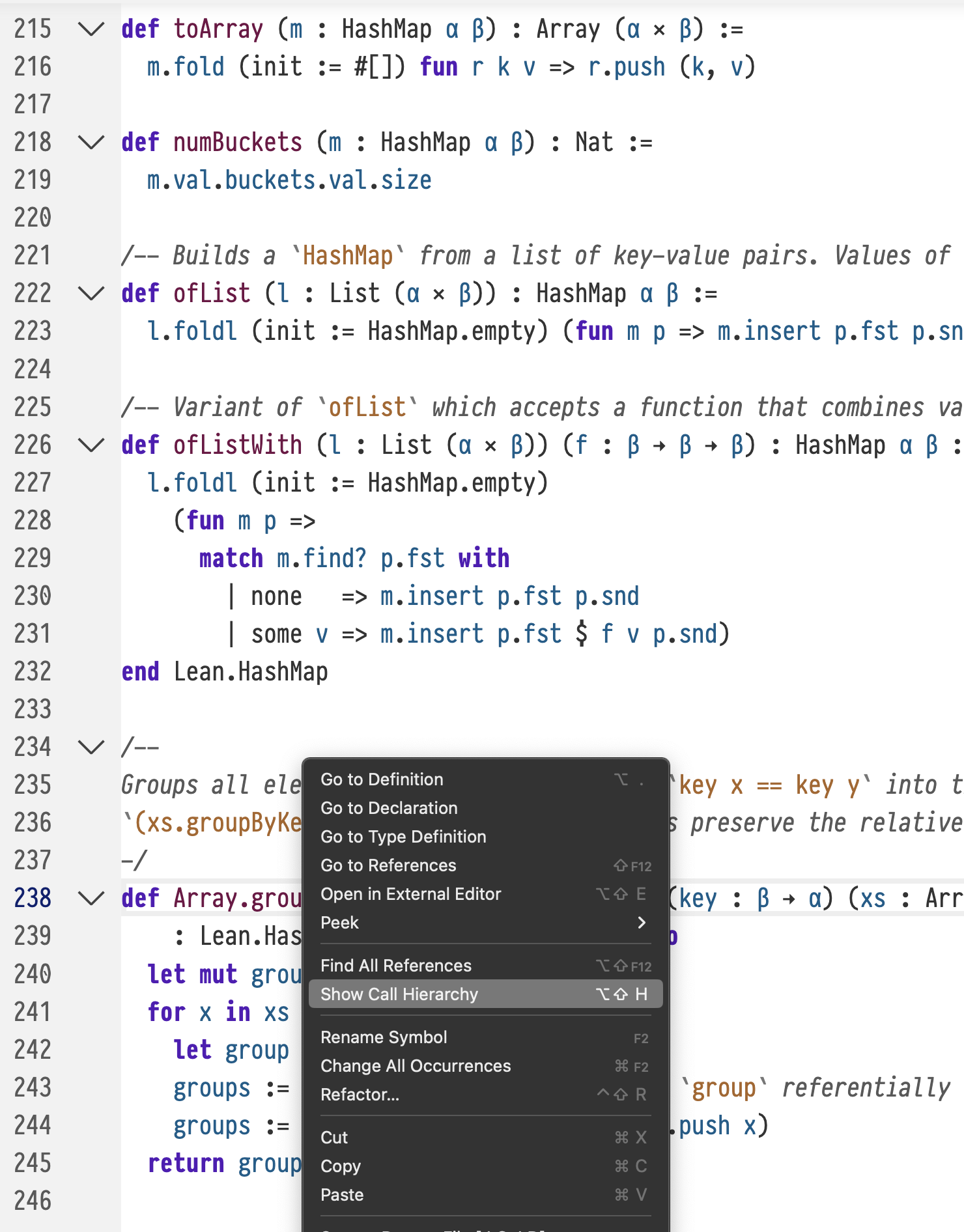
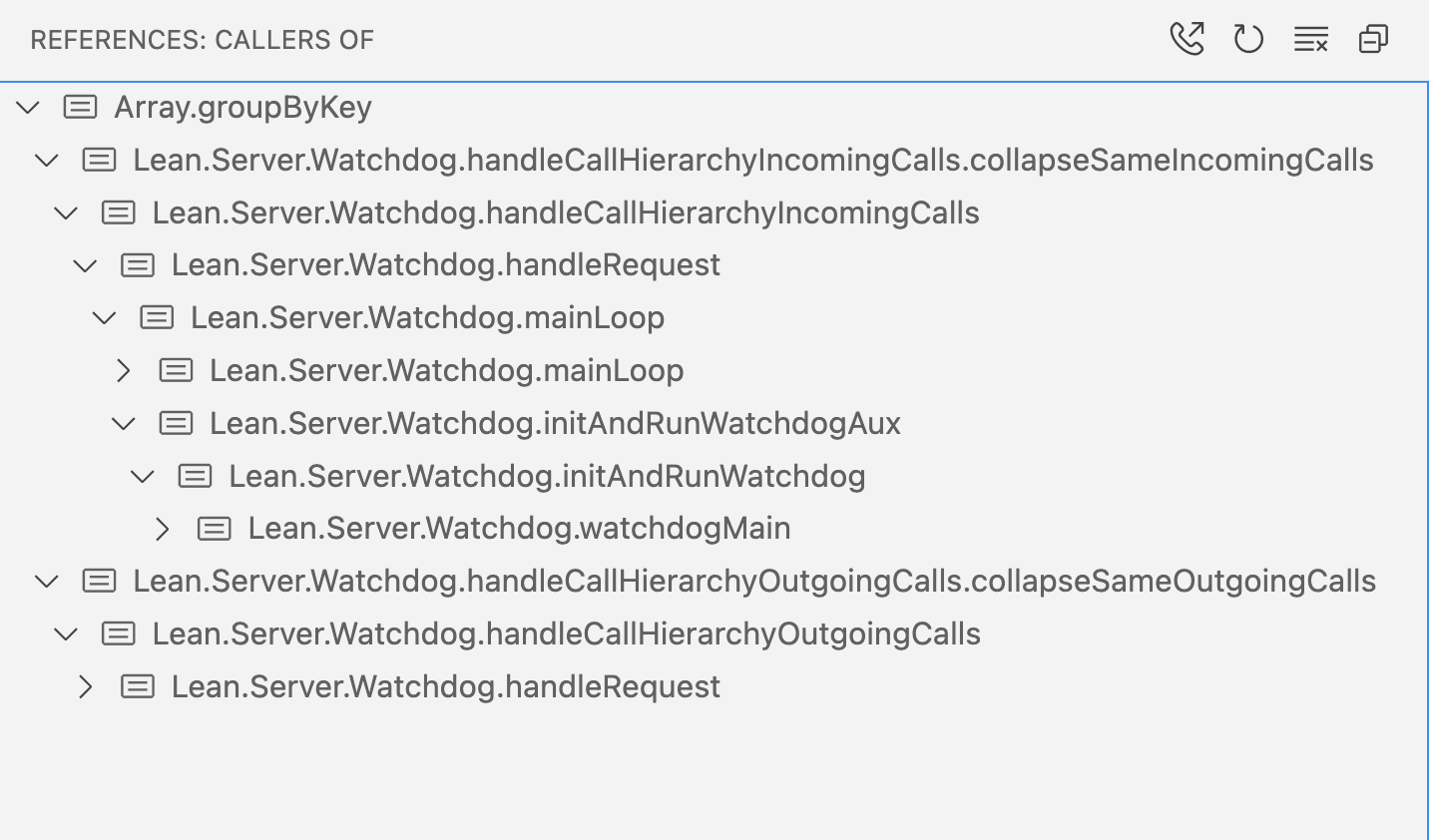
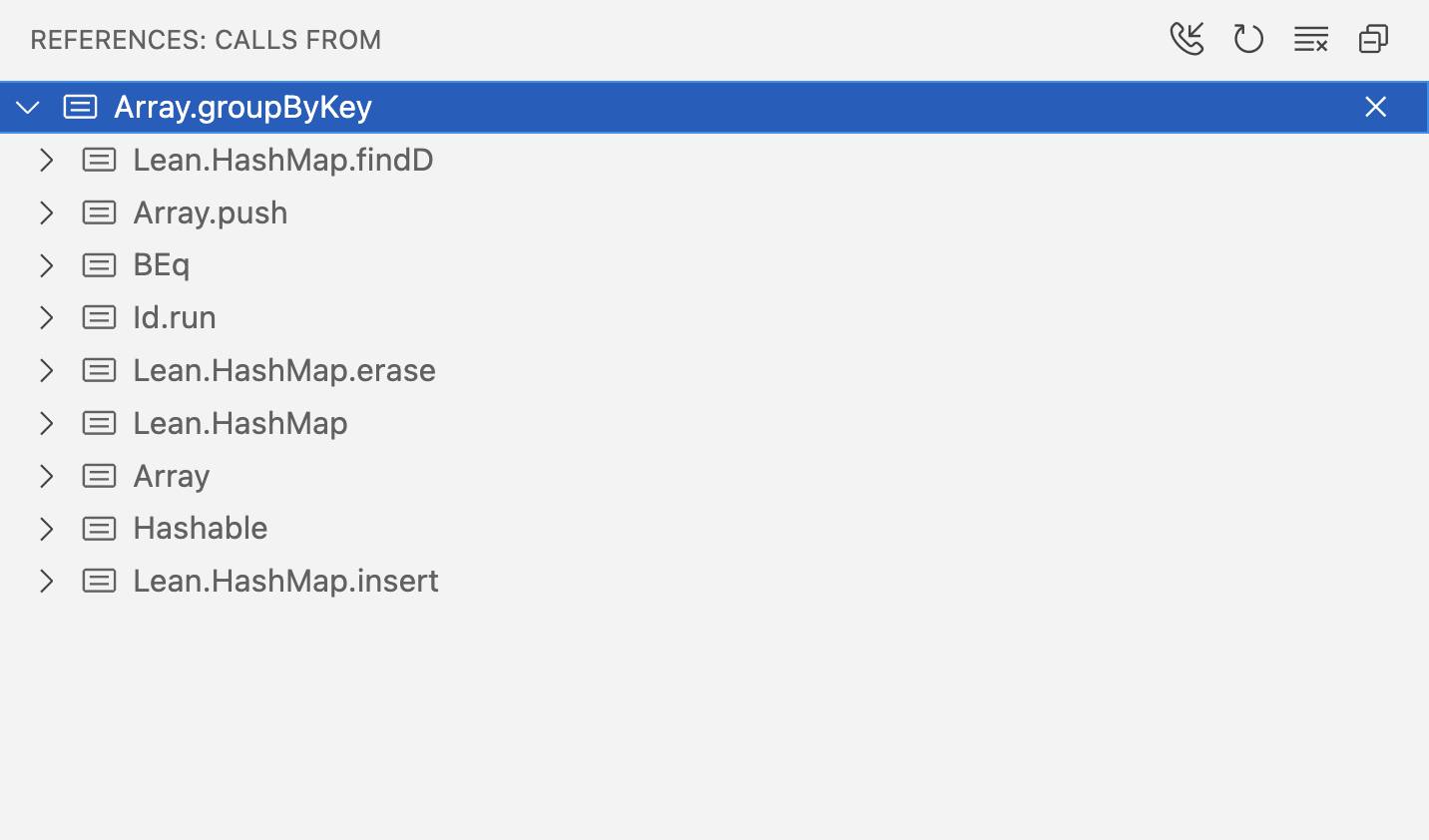
Lean's language server now supports call hierarchy queries. This makes it easy to find out who calls a given function, and recursively explore their callers and their callers' callers.

In VSCode, it looks like this:

Invoking call hierarchy

The call hierarchy view can be invoked from a context menu, or with keyboard shortcuts

Outgoing call hierarchy

By default, outgoing calls are shown

Incoming call hierarchy

Incoming calls can be shown as well, to explore "backwards"

Pretty Printer

Lean's pretty printer is the component of the system that's responsible for rendering terms in proof goals, error messages, and other communication to users. Because it is used in so many different contexts, the pretty printer has a number of configurable options that can be used to make it fit a particular use case. Based on user request, new options were introduced in this release.

Sometimes, a term may be very large, but the part that's relevant to the task at hand is not deeply buried. In these cases, the following pretty-printer options can be used:

  • If pp.deepTerms is set to false, the pretty printer stops printing at a given depth in the tree, replacing the term with an ellipsis.

  • When deep terms are to be elided, the threshold is specified in pp.deepTerms.threshold.

For example, take the following definition of a tree datatype and a function that generates a large tree:

inductive Tree (α) where | leaf | branch (left : Tree α) (val : α) (right : Tree α) def Tree.count : Tree α → Nat | .leaf => 0 | .branch l _ r => l.count + r.count + 1 def unbalanced (n : Nat) : Tree Nat := if n = 0 then .leaf else let left := unbalanced (n / 2) let right := unbalanced (n - 1) .branch left n right termination_by n decreasing_by all_goals
n:Nat
h✝:¬n = 0
⊢ n - 1 < n
;
All goals completed! 🐙

A proof state that contains a large tree is difficult to read and occupies a great deal of space:

example : (unbalanced 10).count = 59 :=
⊢ Tree.count (unbalanced 10) = 59
⊢ Tree.count (Tree.branch (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)) 5 (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)) 4 (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 3 (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf))))) 10 (Tree.branch (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)) 4 (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 3 (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)))) 9 (Tree.branch (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)) 4 (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 3 (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)))) 8 (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 3 (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf))) 7 (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 3 (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf))) 6 (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)) 5 (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)) 4 (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 3 (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)))))))))) = 59
unsolved goals
⊢ Tree.count
      (Tree.branch
        (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)) 5
          (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)) 4
            (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 3
              (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)))))
        10
        (Tree.branch
          (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)) 4
            (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 3
              (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf))))
          9
          (Tree.branch
            (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)) 4
              (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 3
                (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf))))
            8
            (Tree.branch
              (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 3
                (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)))
              7
              (Tree.branch
                (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 3
                  (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)))
                6
                (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)) 5
                  (Tree.branch (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)) 4
                    (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 3
                      (Tree.branch (Tree.branch Tree.leaf 1 Tree.leaf) 2 (Tree.branch Tree.leaf 1 Tree.leaf)))))))))) =
    59

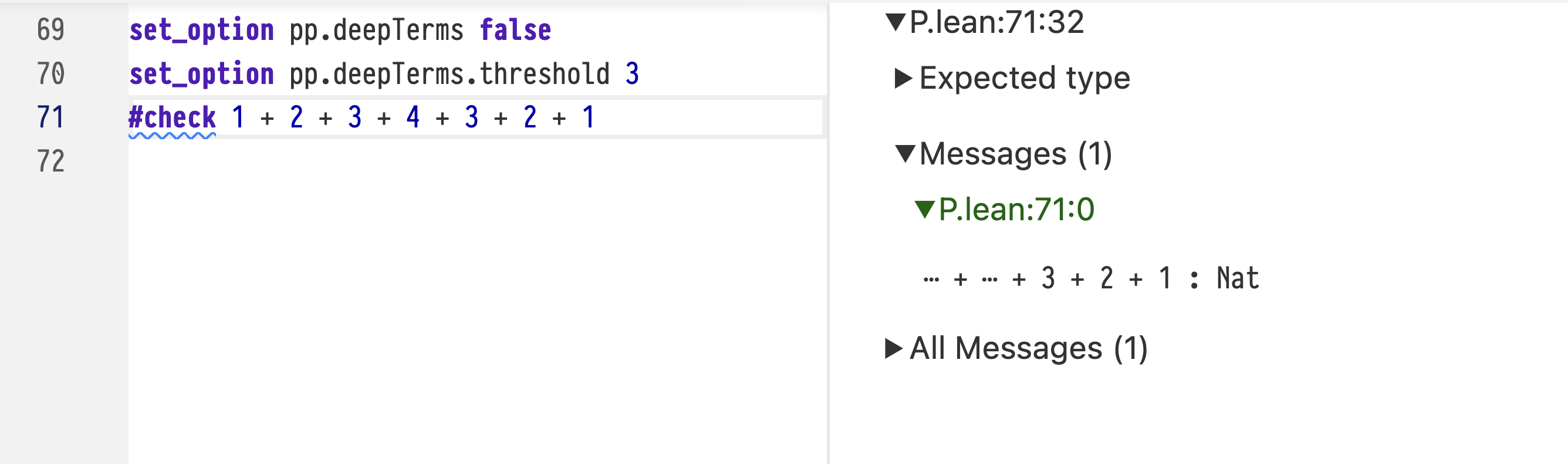
Asking Lean to elide deep terms and setting a suitable threshold greatly reduces the size of the message:

set_option pp.deepTerms false set_option pp.deepTerms.threshold 5 example : (unbalanced 10).count = 59 :=
⊢ Tree.count (unbalanced 10) = 59
⊢ Tree.count (Tree.branch (Tree.branch (Tree.branch (Tree.branch ⋯ ⋯ ⋯) 2 (Tree.branch ⋯ ⋯ ⋯)) 5 (Tree.branch (Tree.branch ⋯ ⋯ ⋯) 4 (Tree.branch ⋯ ⋯ ⋯))) 10 (Tree.branch (Tree.branch (Tree.branch ⋯ ⋯ ⋯) 4 (Tree.branch ⋯ ⋯ ⋯)) 9 (Tree.branch (Tree.branch ⋯ ⋯ ⋯) 8 (Tree.branch ⋯ ⋯ ⋯)))) = 59
unsolved goals
⊢ Tree.count
      (Tree.branch
        (Tree.branch (Tree.branch (Tree.branch ⋯ ⋯ ⋯) 2 (Tree.branch ⋯ ⋯ ⋯)) 5
          (Tree.branch (Tree.branch ⋯ ⋯ ⋯) 4 (Tree.branch ⋯ ⋯ ⋯)))
        10
        (Tree.branch (Tree.branch (Tree.branch ⋯ ⋯ ⋯) 4 (Tree.branch ⋯ ⋯ ⋯)) 9
          (Tree.branch (Tree.branch ⋯ ⋯ ⋯) 8 (Tree.branch ⋯ ⋯ ⋯)))) =
    59

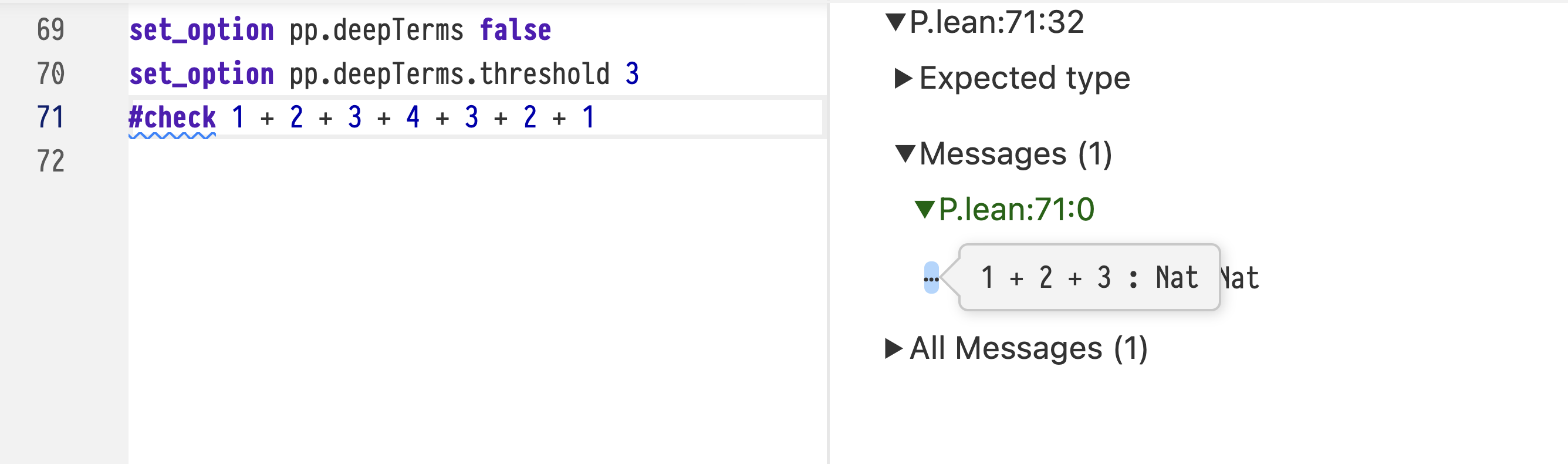
Hovering the mouse over an ellipsis shows the elided term:

Elided term in infoview

Terms that exceed the depth specified with pp.deepTerms.threshold are replaced by an ellipsis.

Elided term in infoview with hover

The elided terms are still visible by hovering the mouse over them.

Additionally, Lean's pretty printer now supports adding type annotations to numeric literals. In this example, there's no way to see the types by glancing at the output:

structure Numbers where one : Nat another : Int yetMore : Float { one := 3, another := 3, yetMore := 3 } : Numbers#check {one := 3, another := 3, yetMore := 3 : Numbers}
{ one := 3, another := 3, yetMore := 3 } : Numbers

Setting pp.numeralTypes to true results in type ascriptions:

set_option pp.numericTypes true { one := (3 : Nat), another := (3 : Int), yetMore := (3 : Float) } : Numbers#check {one := 3, another := 3, yetMore := 3 : Numbers}
{ one := (3 : Nat), another := (3 : Int), yetMore := (3 : Float) } : Numbers

Further Improvements

Further improvements were made to the pretty printer, Lake's handling of multiple-platform projects, and the behavior of Array.swap! was made more consistent with the other !-variants. The implementation of structure updating was made both more predictable and faster, which led to a large improvement in Mathlib's build times. Many small bugs were fixed, and many more improvements were made—please see the release notes for a complete list.