Lean 4.12.0
We are pleased to announce the release of Lean version 4.12.0! This release includes significant additions to tactics, performance, and Lake packages.
Please see the detailed release notes for the complete list of changes.
Bitvector Tactic: bv_decide
Lean 4.12.0 introduces the powerful bv_decide tactic, designed to simplify and automate proofs involving bitvectors (BitVec) and booleans (Bool). This tactic reduces goals to a satisfiability (SAT) problem, which is then refuted using an external SAT solver.
It is capable of handling complex, real-world problems, such as AWS's LNSym project for verifying cryptographic primitives implemented in ARM assembly.
An example of using bv_decide is verifying that a bit-twiddling formula leaves at most one bit set:
def popcount (x : BitVec 64) : BitVec 64 :=
let rec go (x pop : BitVec 64) : Nat → BitVec 64
| 0 => pop
| n + 1 => go (x >>> 2) (pop + (x &&& 1)) n
go x 0 64
example (x : BitVec 64) : popcount ((x &&& (x - 1)) ^^^ x) ≤ 1 := x:BitVec 64⊢ popcount (x &&& x - 1 ^^^ x) ≤ 1
x:BitVec 64⊢ ⋯ + ⋯ + (⋯ &&& 1) + (⋯ >>> 2 &&& 1) + (⋯ >>> 2 >>> 2 &&& 1) + (⋯ >>> 2 >>> 2 >>> 2 &&& 1) +
(⋯ >>> 2 >>> 2 >>> 2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) +
(⋯ >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>> 2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 >>>
2 &&&
1) ≤
1
All goals completed! 🐙
If the external solver cannot refute the SAT instance, bv_decide provides a counterexample, aiding in debugging:
example (x : BitVec 64) : x < x + 1 := x:BitVec 64⊢ x < x + 1
All goals completed! 🐙The prover found a potential counterexample, consider the following assignment: x = 0xffffffffffffffff#64
Lean now ships with the CaDiCaL SAT solver built-in, so no external tooling is required to run bv_decide.
The SAT solver produces an LRAT proof that is checked within Lean via verified algorithms. Proofs generated by this tactic use the Lean.ofReduceBool axiom, so this tactic includes the Lean compiler as part of the trusted code base.
The bv_decide tactic streamlines reasoning about low-level bitvector manipulations, making it an invaluable tool for formal verification tasks.
More information is available in the Language features, tactics, and metaprograms section.
Unified Equational Theorems for Definitions
In Lean 4.12.0, we've unified the handling of equational lemmas for both recursive and non-recursive definitions. Previously, non-recursive functions defined by pattern matching had their own set of equational lemmas, which differed from those of recursive functions. Now, all functions benefit from a consistent set of equational lemmas, enhancing predictability and ease of use.
For example, consider the Option.map function:
def Option.map (f : α → β) : Option α → Option β | some x => some (f x) | none => none
Lean now generates the following equational lemmas:
-
Option.map.eq_1 (f : α → β) (x : α) : Option.map f (some x) = some (f x) -
Option.map.eq_2 (f : α → β) : Option.map f none = none -
Option.map.eq_def (f : α → β) (x : Option α) : Option.map f x = match x with | some y => some (f y) | none => none -
Option.map.eq_unfold:@Option.map=fun {α} {β} (f : α → β) x => match x with | some x => some (f x) | none => none
The eq_unfold lemma is particularly useful for rewriting under binders using rw. This unification simplifies reasoning about functions and reduces the need to remember different behaviors for different kinds of definitions.
Performance Improvements
Lean 4.12.0 includes several performance optimizations that make the system more responsive and efficient:
- Optimized Expression Handling
Improvements in the kernel's expression equality tests and caching mechanisms reduce overhead in type-checking and elaboration.
- Enhanced Diagnostics
New profiling tools help identify and diagnose performance bottlenecks in large proofs, enabling users to optimize their code more effectively.
- Rewritten Core Algorithms
Certain key functions like
Lean.instantiateLevelMVarsandLean.instantiateExprMVarshave been reimplemented resulting in performance boosts of up to 30% in benchmarks.
Please see Lean Internals → Performance for more information.
Library Enhancements
Our standard library has been significantly expanded and improved:
- List and Array Modules
Numerous lemmas have been added to
ListandArray, including properties ofList.find?,List.Sublist,List.mergeSort, andList.attach. This API works continues to build on existing contributions by many authors in the Mathlib and Batteries libraries.- BitVector Enhancements
The
BitVecmodule now includes new definitions and lemmas, including bitblasting support forbv_decide. These improvements support more sophisticated manipulations of bitvectors.-
Std.HashMapandStd.HashSetUpdates We've continued to refine our hash map and hash set implementations, deprecating older versions in favor of
Std.HashMapandStd.HashSet. These structures are now used throughout Lean's library.- Parsec Generalization
The
Std.Internal.Parseclibrary has been generalized to allow parsing of iterable data beyond strings, such asByteArray.
Please see the Library section of the release notes for more information.
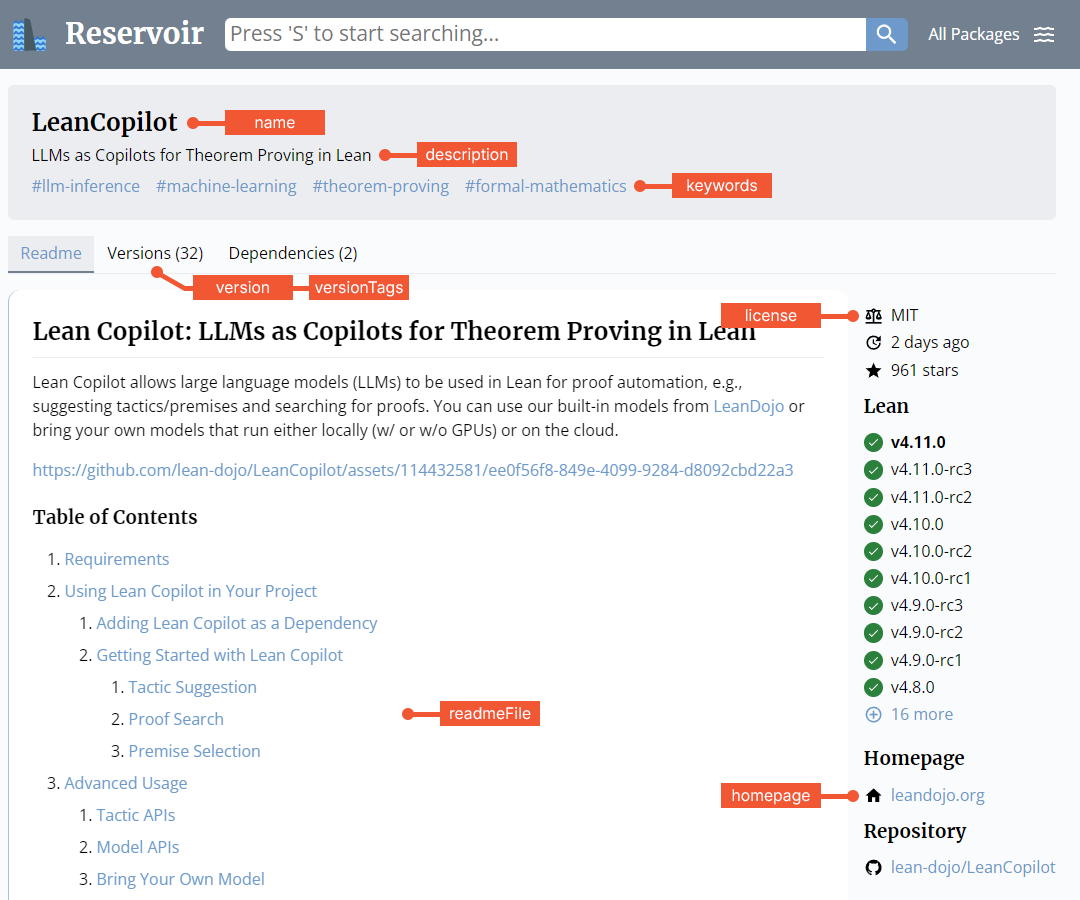
Lake and Reservoir
Packages now have versioning and we recommend all package authors to use this new capability. In v4.12.0, Lake has added a number of package configuration options which can be used to control how Reservoir indexes and displays packages.
If a Reservoir setting is not configured in Lake, Reservoir will use information from the package's GitHub repository to fill in missing details (e.g., description, homepage, keywords from labels, etc.).
See the doc-strings of these options for detailed explanations.
Versions indicate how a package has changed and using the package version field helps you describe those changes to users.
In Lake, versions have the form:
<major>.<minor>.<patch>[-<specialDescr>]
The different version components should be updated to indicate the relative difficulty of updating the package.
Changes in the minor version should generally come with deprecation warnings and/or migration notes.
Changes in the patch version should generally either not require updates to downstream packages, or only changes driven by deprecation warnings or other code actions.
A version with a - suffix is considered a "prerelease". It is usually used for revisions of package between different revisions (e.g., the RCs of Lean).
The first official release of a package should start at version 1.0.0 and continue from there.
Reservoir indexes GitHub repositories, but not every revision within them. Reservoir uses the repository's Git tags filtered by the versionTags option. The option specifies which tags represented versions. By default, Reservoir treats tags that start with v followed by a digit as versions (e.g., v4.12.0 or v3-eol, but not nightly-testing-2024-09-30).
Breaking Changes
While we're working towards stronger backward compatibility guarantees, many changes in Lean 4.12.0 may require updates to existing code:
- LibUV Dependency
Lean now requires LibUV for building from source. Developers compiling Lean themselves should install LibUV as per the updated build instructions.
- Equational Lemma Changes
The unification of equational lemmas means that functions may have additional or renumbered lemmas. Code relying on specific lemma names (e.g.,
f.eq_2) may need adjustment.-
reduceCtorEqSimproc This simplification procedure is now optional and might need to be explicitly included in
simpcalls (e.g.,simp only [reduceCtorEq]) if required.- Membership Parameter Order
The parameters for
Membership.memhave been swapped. This affects all instances ofMembershipand may require code updates whereMembership.memis used.- Parsec Library Location
The
Std.Internal.Parseclibrary has moved fromLean.Data.ParsectoStd.Internal.Parsec. Users should update their imports accordingly.- Deprecated HashMap and HashSet
Lean.HashMapandLean.HashSetare now deprecated in favor ofStd.HashMapandStd.HashSet. Users should migrate to the new implementations to avoid future compatibility issues.
Conclusion
Lean 4.12.0 is rapidly growing as a programming language and theorem prover. We're excited by the possibilities offered by new the new bv_decide tactic. We've been working hard on performance optimizations, and an enriched standard library.
We encourage all users to upgrade to Lean 4.12.0 to take advantage of these improvements. As always, we welcome feedback and contributions from the community to help make Lean even better.
For a complete list of changes and more detailed information, please refer to the official release notes.